Last updated: 2017-12-21

Code version: 6e42447

Simulated correlated data

\[ z_i = L_i^Tx / \sqrt{L_i^TL_i} \ , \] where both \(x\) and \(L_i\) are \(d\)-dimentional independent \(N(0,1)\) random variates, and a large number of \(z_i\) are generated by the same \(x\) and different, independent \(L_i\).

Observation

After extensive exploratory simulations, it seems completely simulated data give cleaner results than simulated real data, which is expected.

source("../code/gdash_lik.R")
set.seed(777)
z.mat <- se.mat <- matrix(0, ncol = 1e4, nrow = 1e3)
for (i in 1 : nrow(z.mat)) {
  L <- matrix(rnorm(1e4 * 10), ncol = 10)
  z.mat[i, ] <- L %*% rnorm(10) / sqrt(rowSums(L^2))
  se.mat[i, ] <- sqrt(rchisq(1e4, 1))
}

Simulation

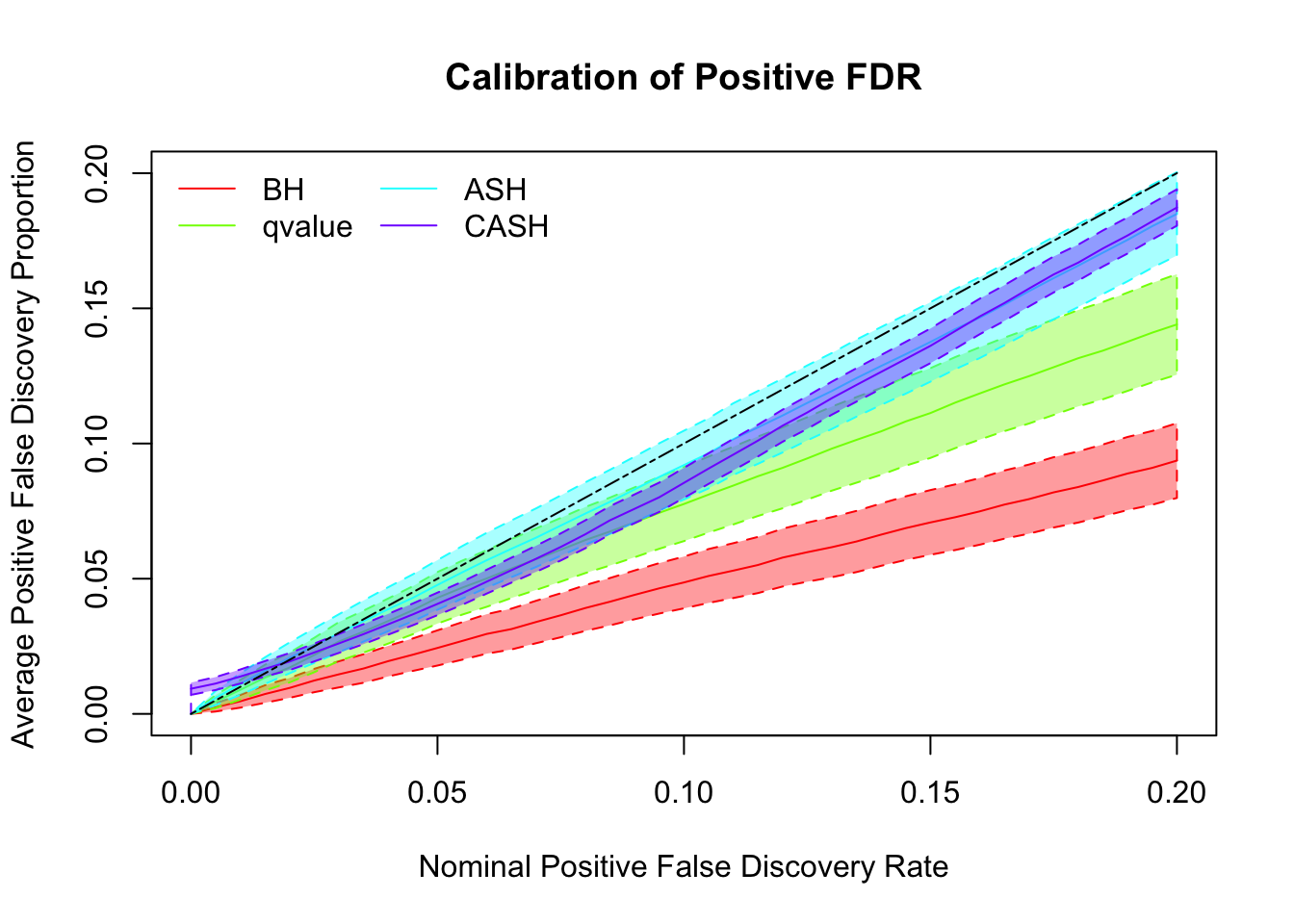
cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.5, 0.3, 0.2), g.sd = c(0, 1, 2), relative_to_noise = FALSE)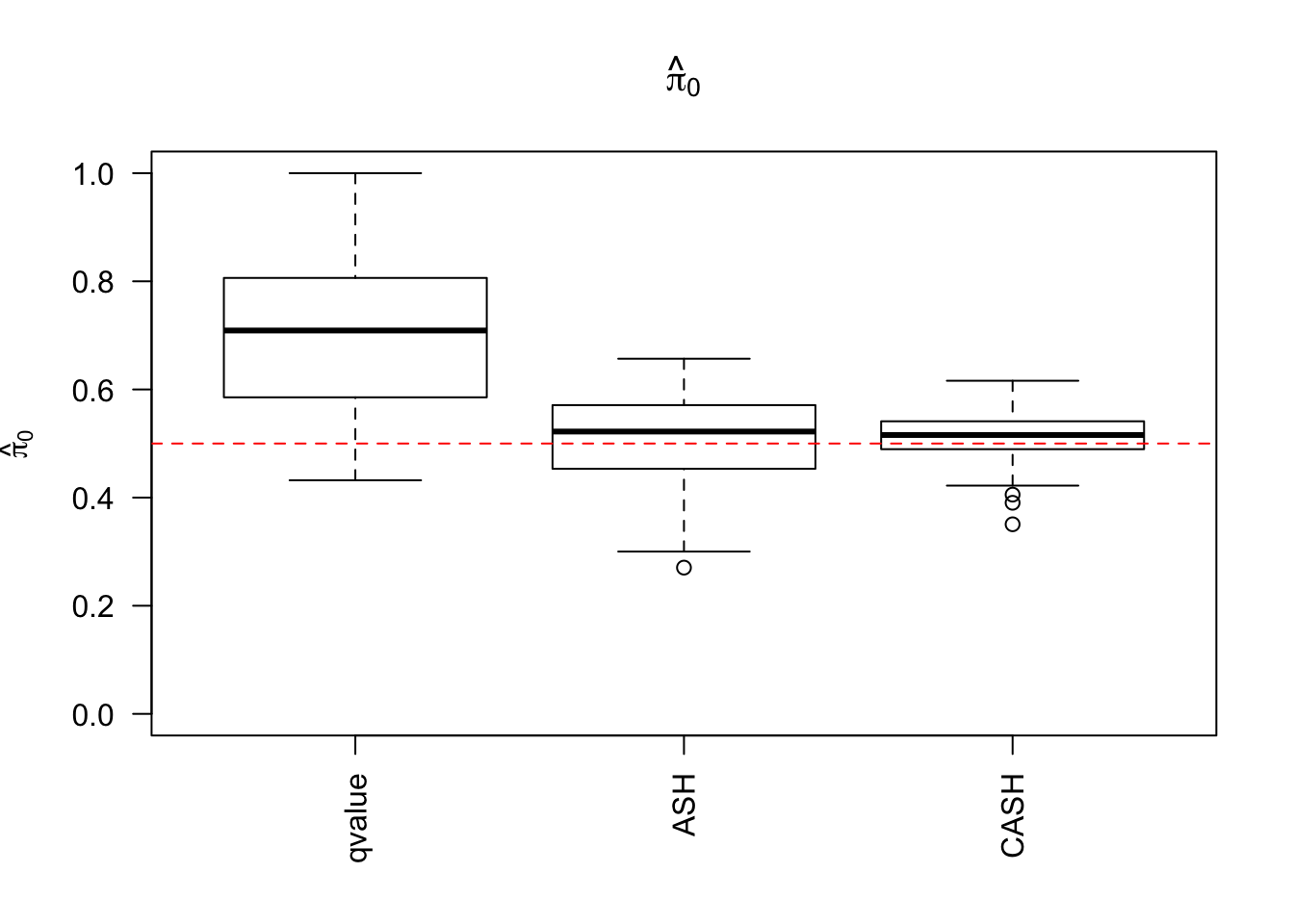

Simulation

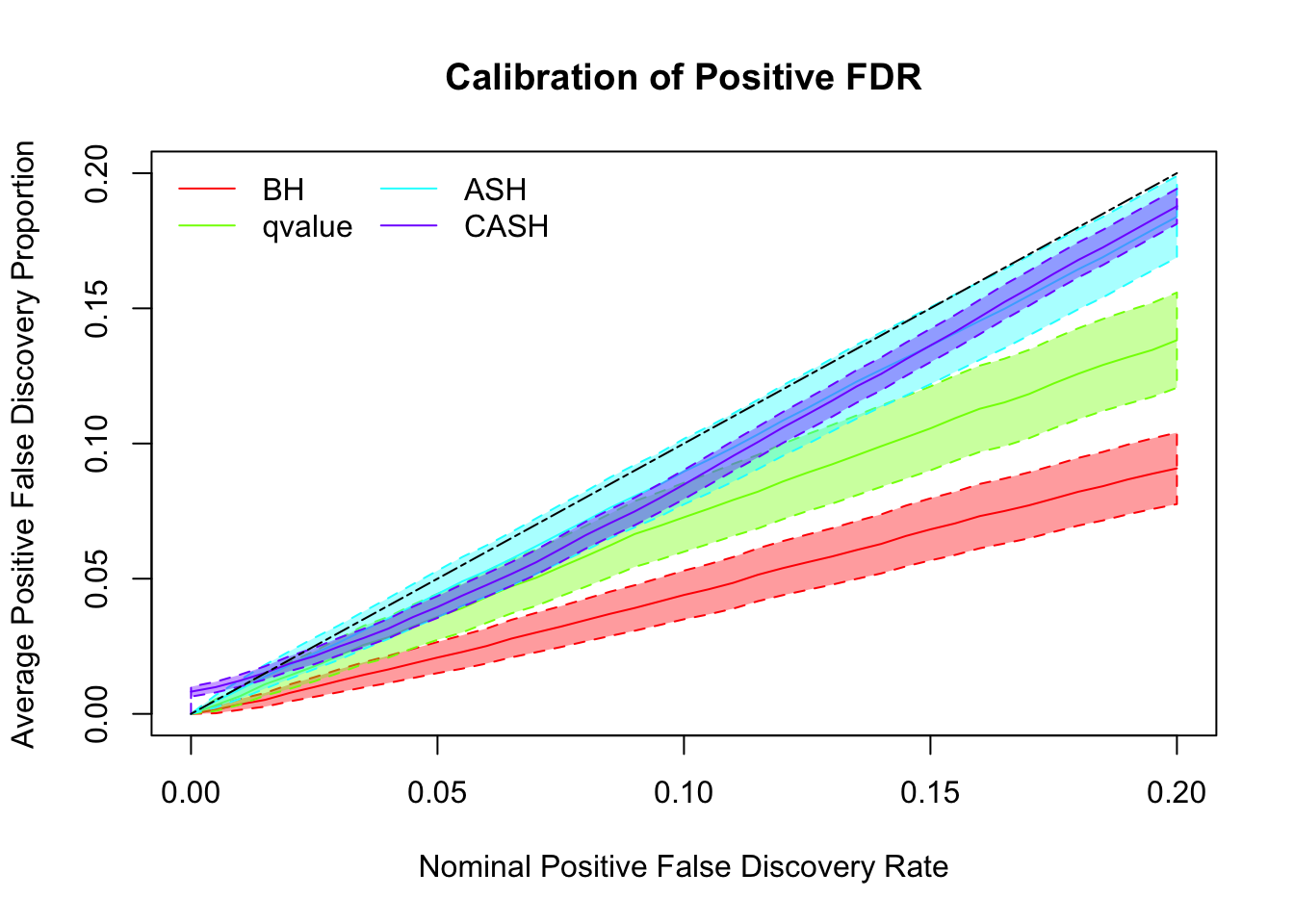
cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.5, 0.4, 0.1), g.sd = c(0, 1, 2), relative_to_noise = FALSE)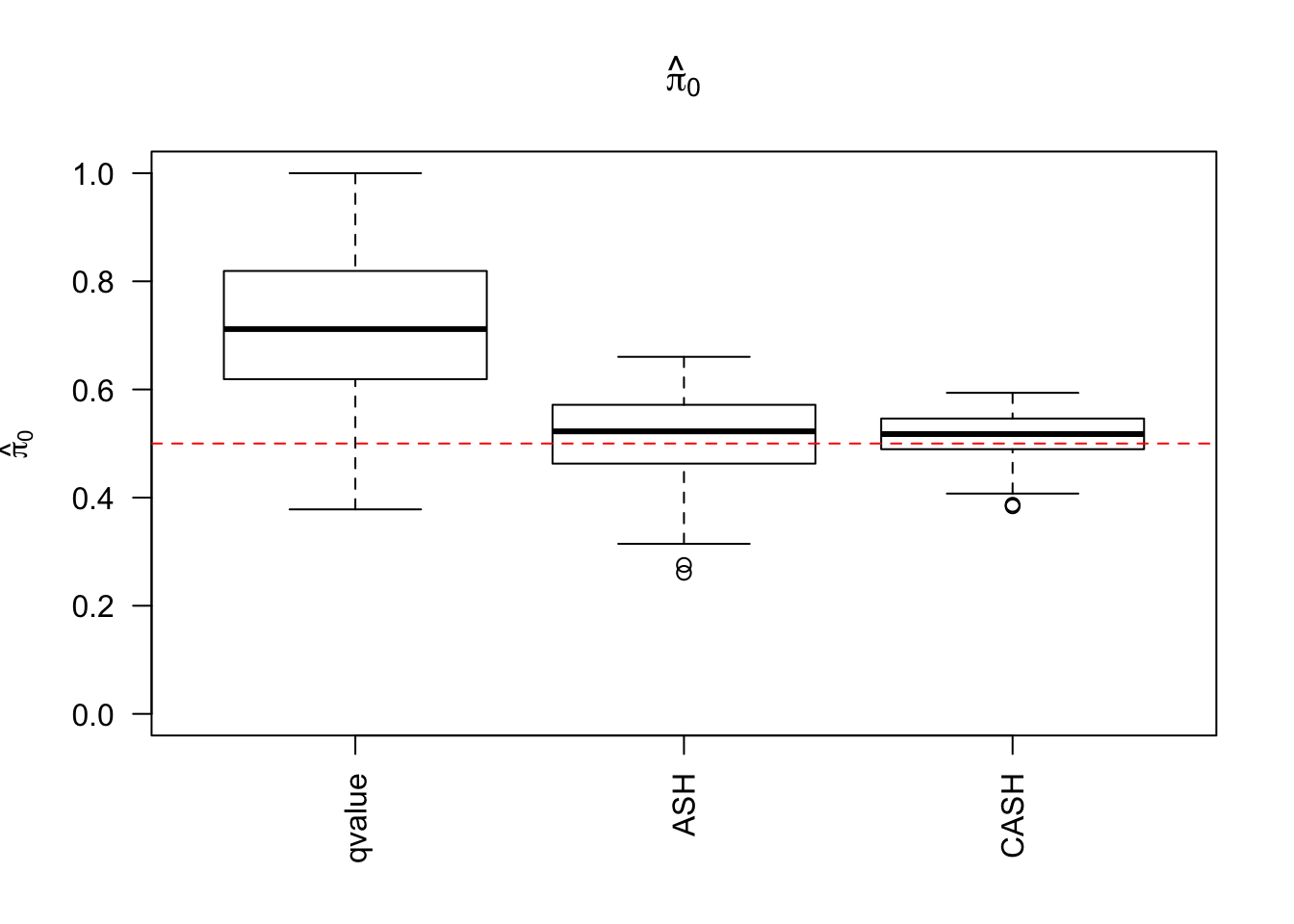

Simulation

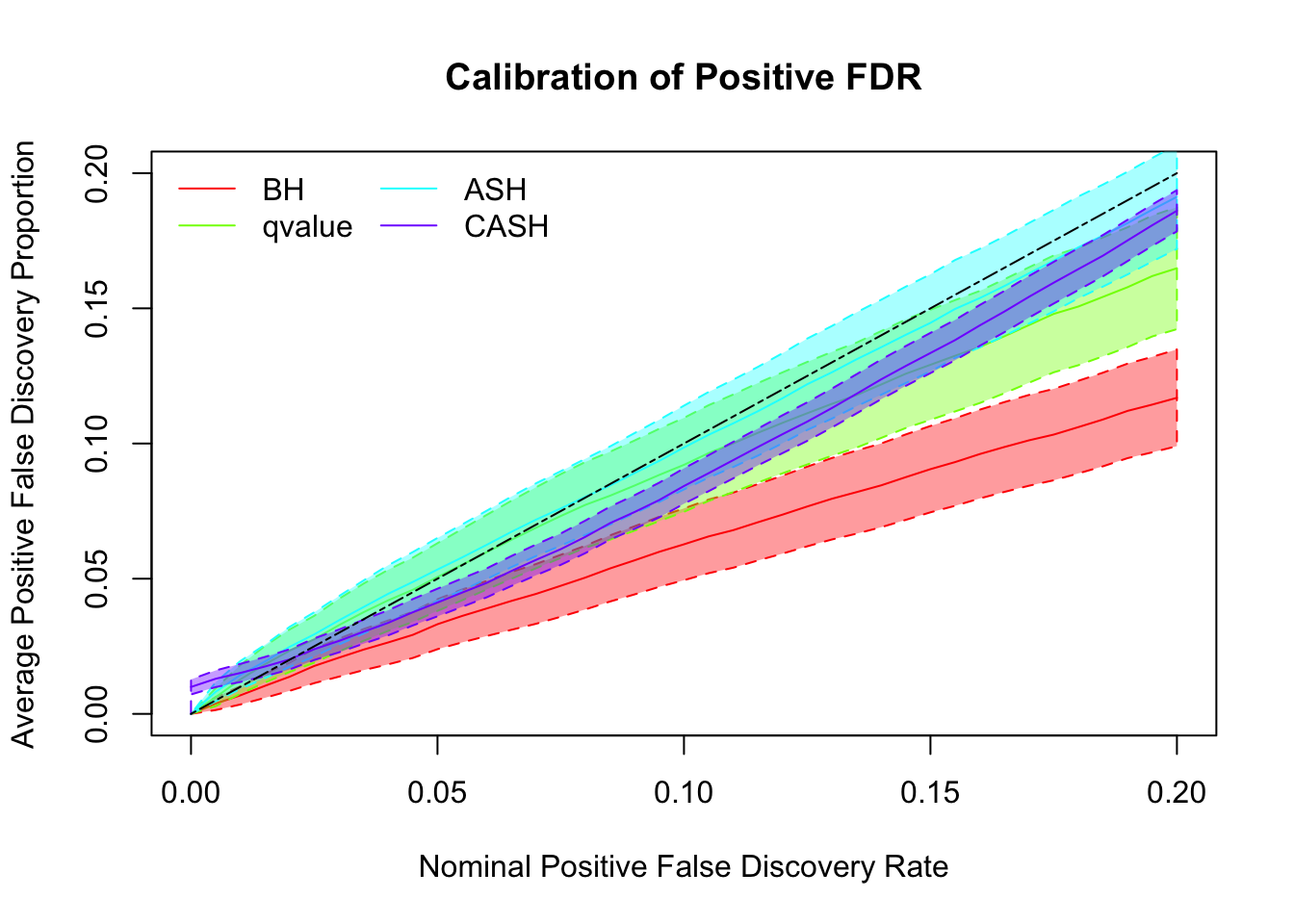
cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.6, 0.3, 0.1), g.sd = c(0, 1, 2), relative_to_noise = FALSE)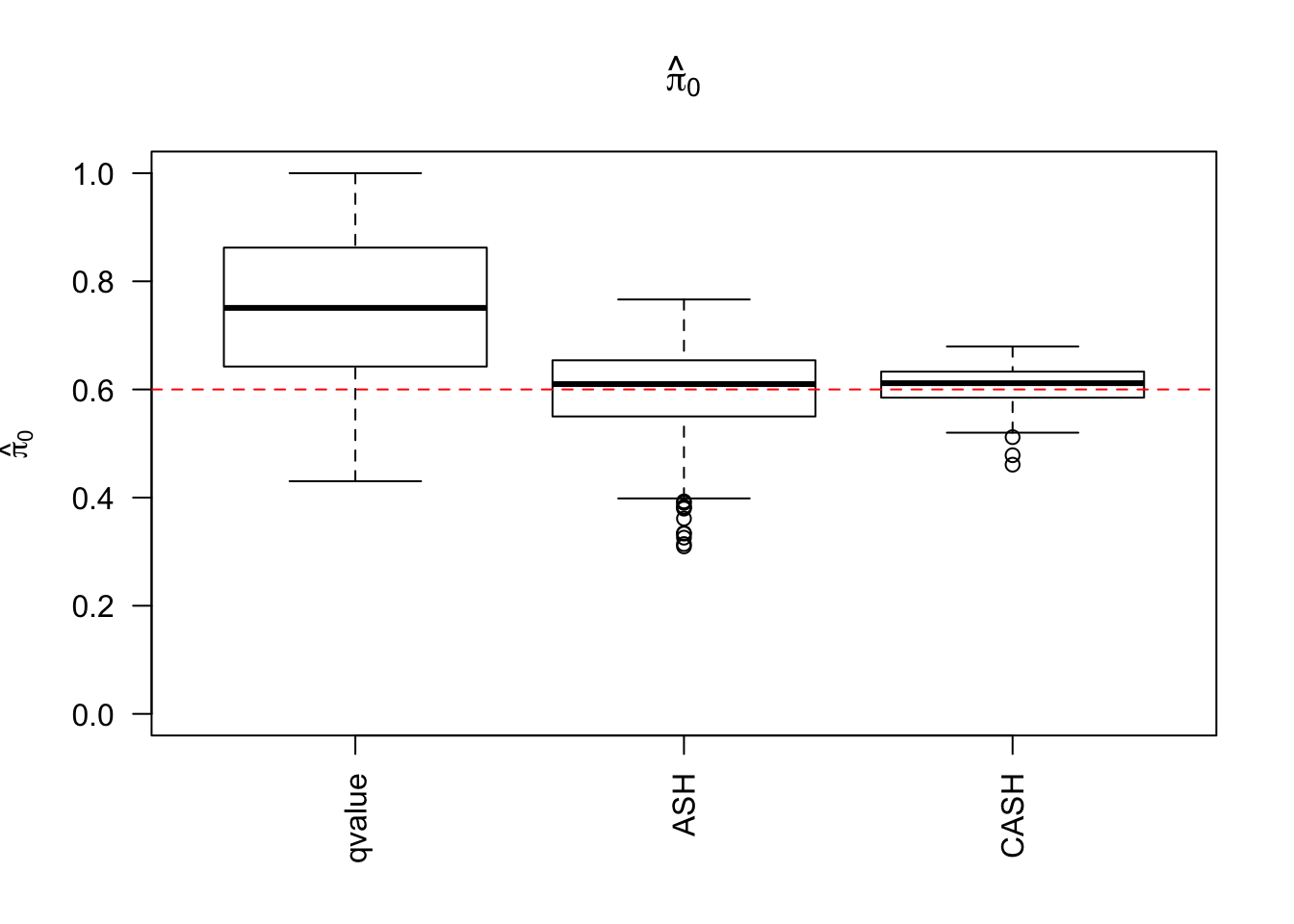

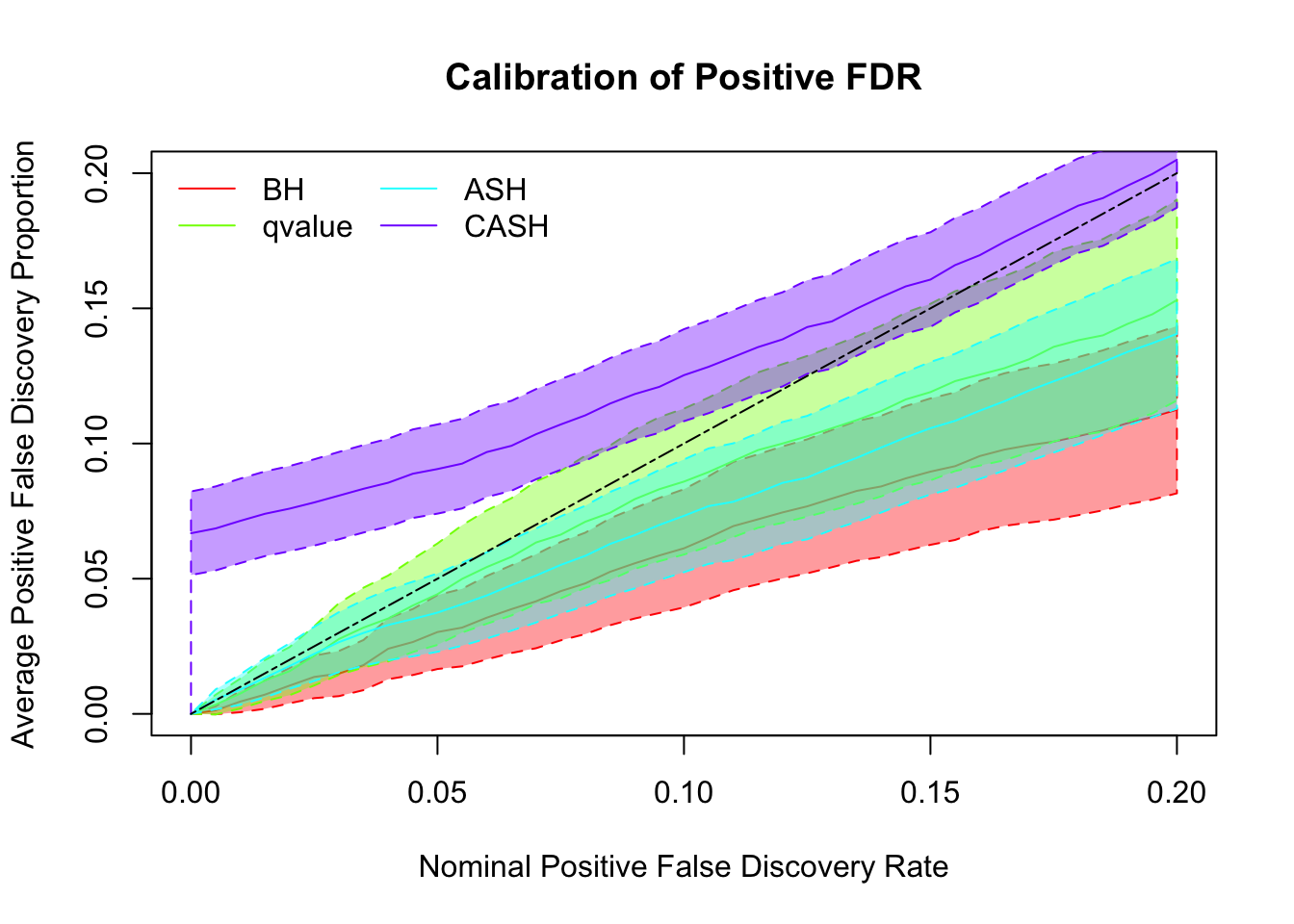
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.1), g.sd = c(0, 1), relative_to_noise = FALSE)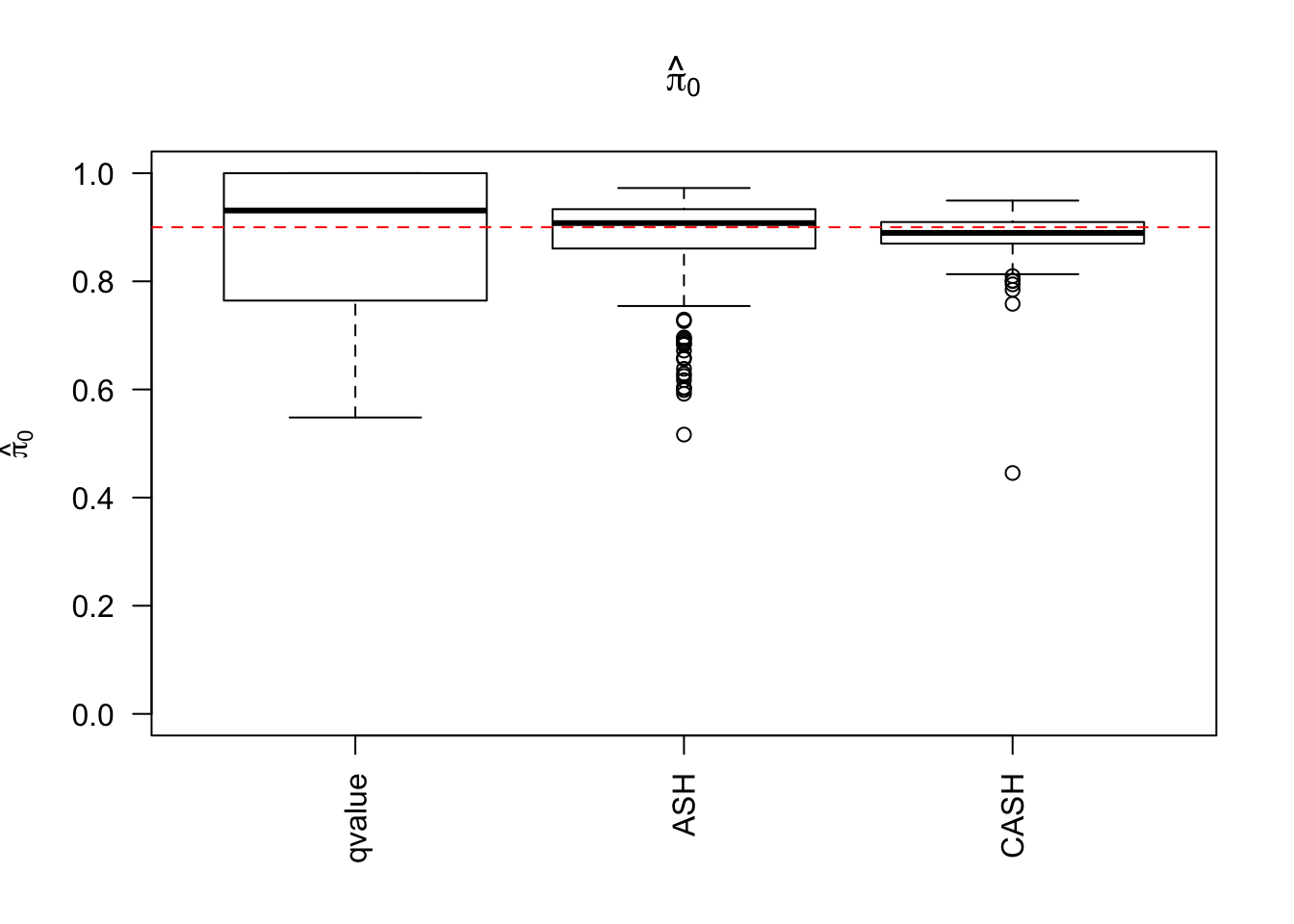

Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.1), g.sd = c(0, 2), relative_to_noise = FALSE)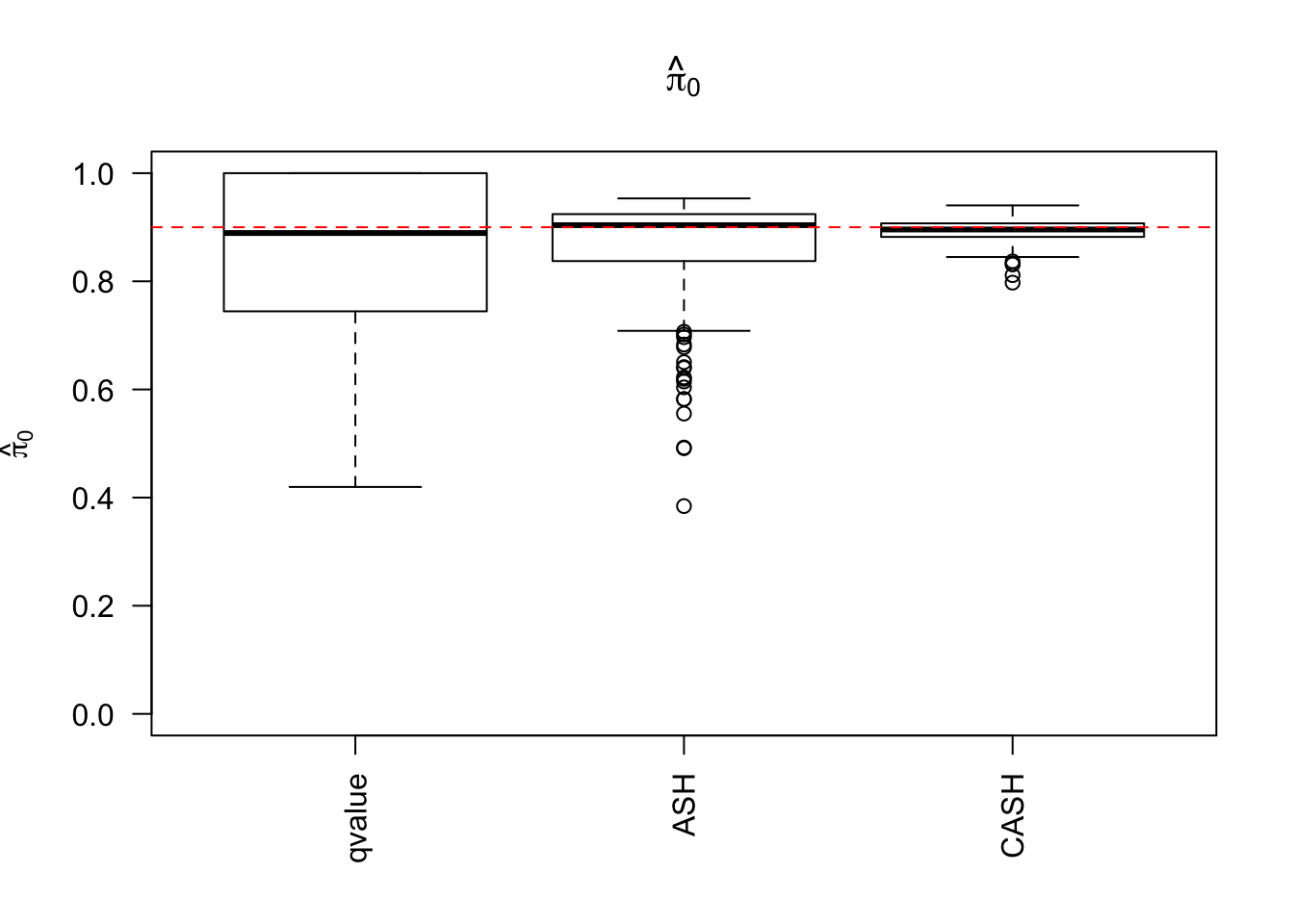

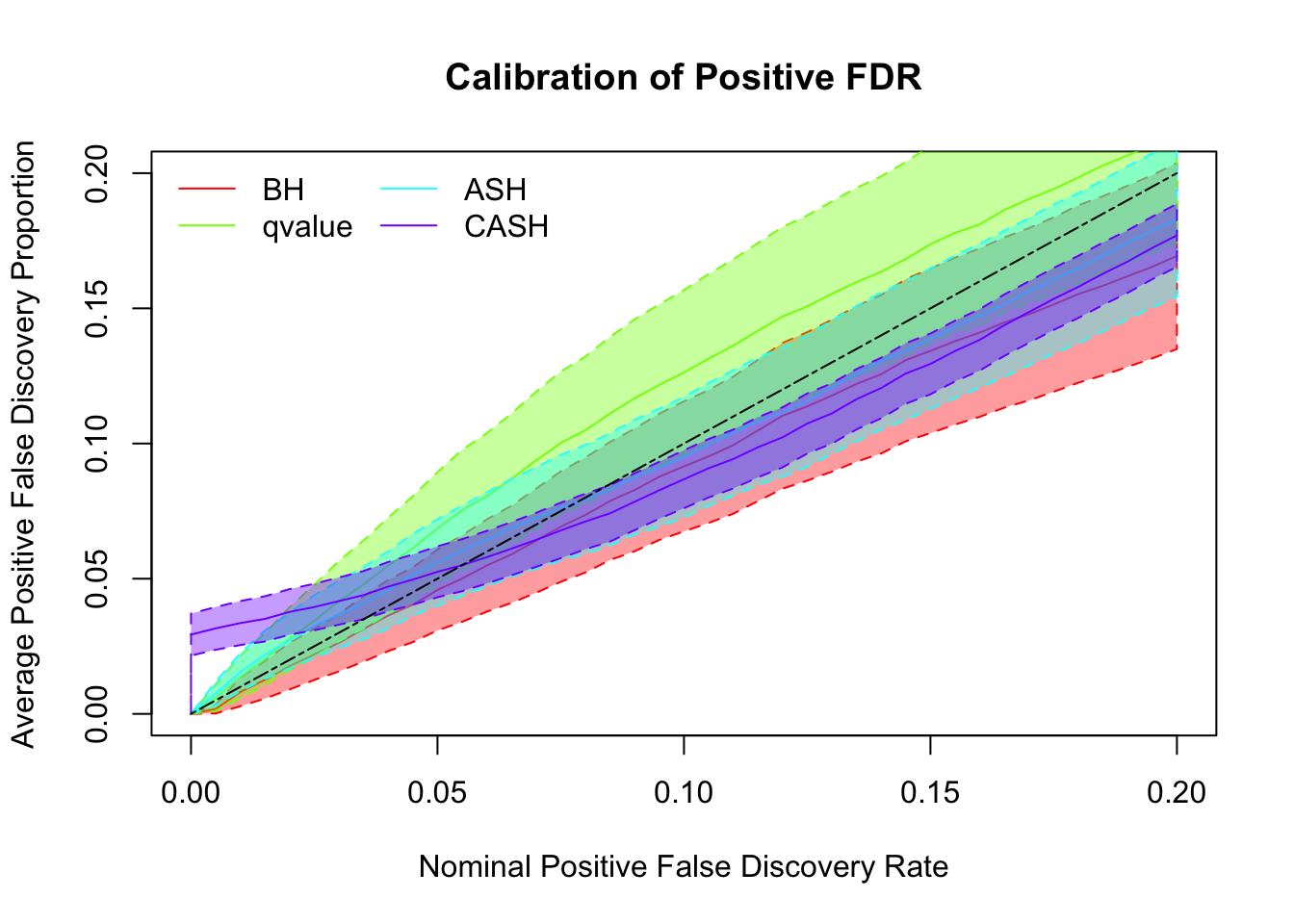
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.1), g.sd = c(0, 3), relative_to_noise = FALSE)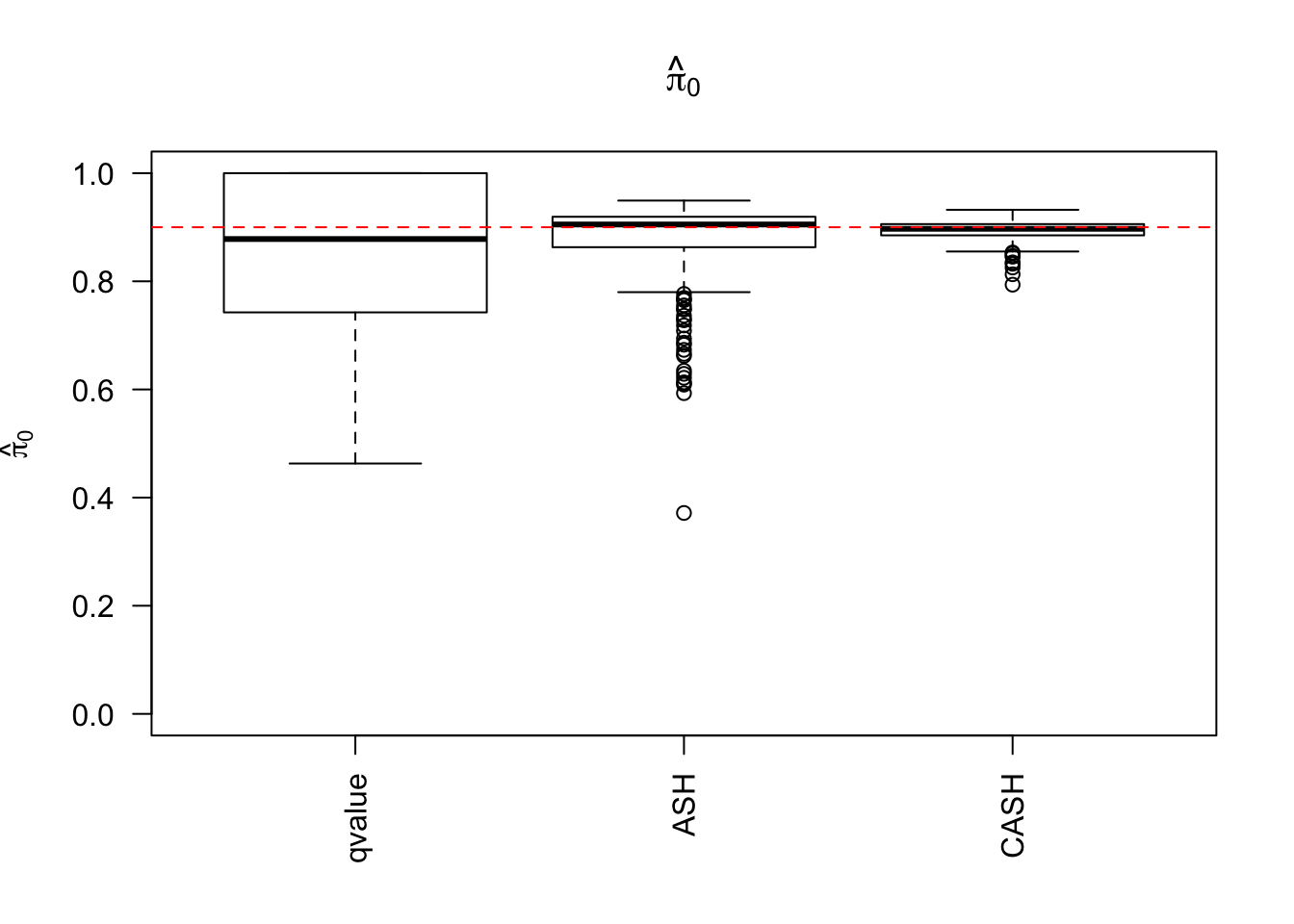

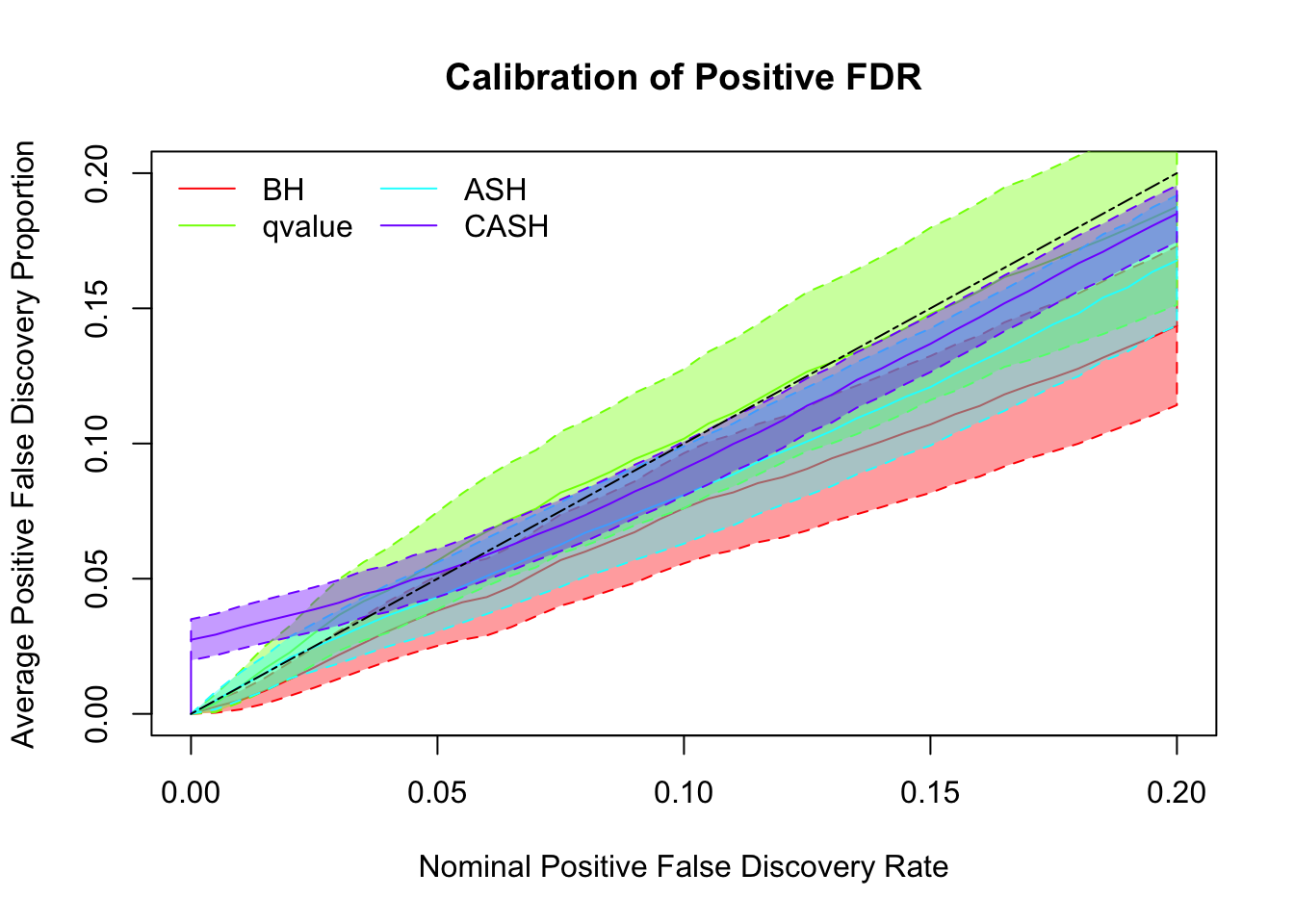
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.05, 0.05), g.sd = c(0, 1, 2), relative_to_noise = FALSE)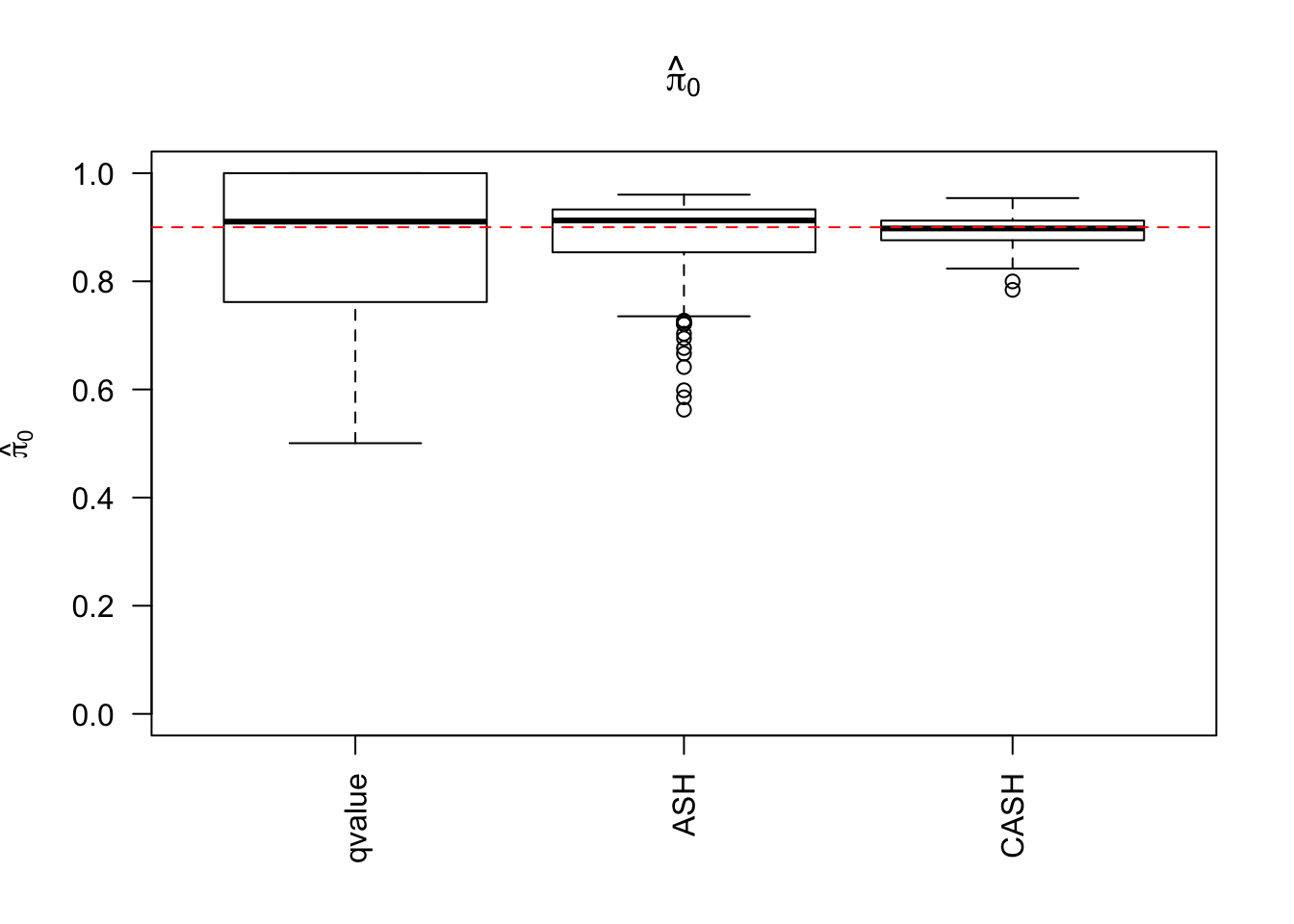

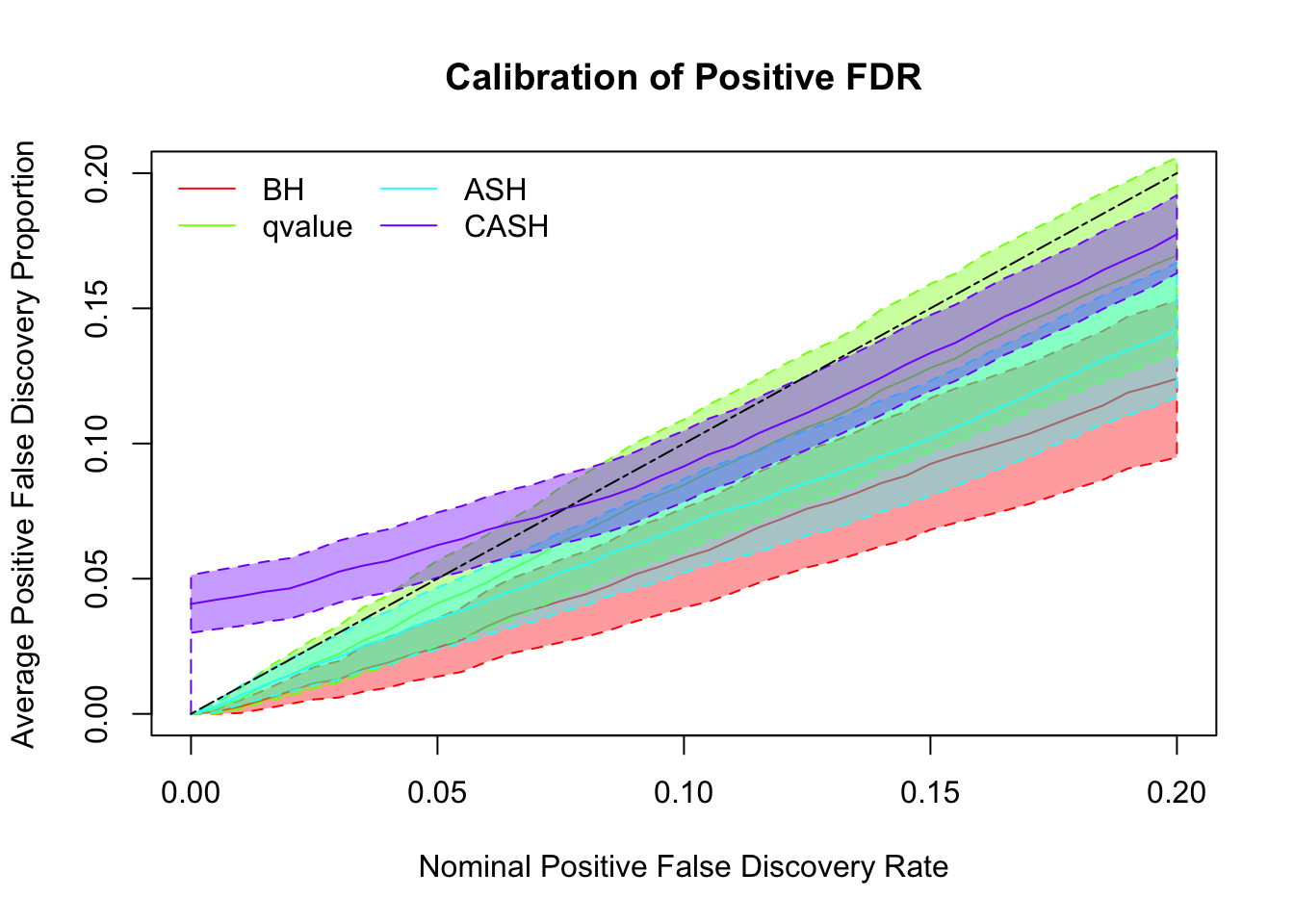
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.05, 0.05), g.sd = c(0, 1, 3), relative_to_noise = FALSE)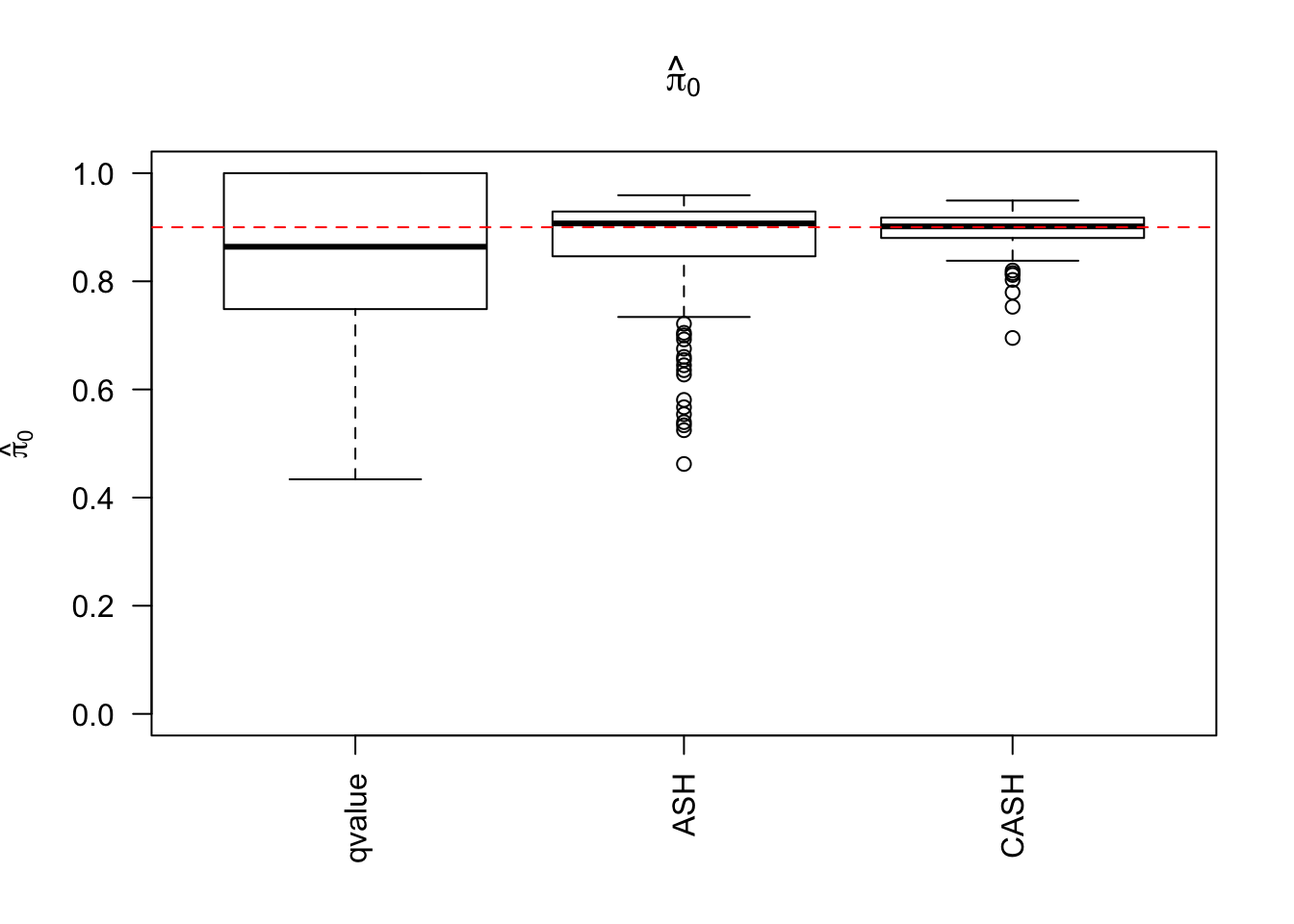

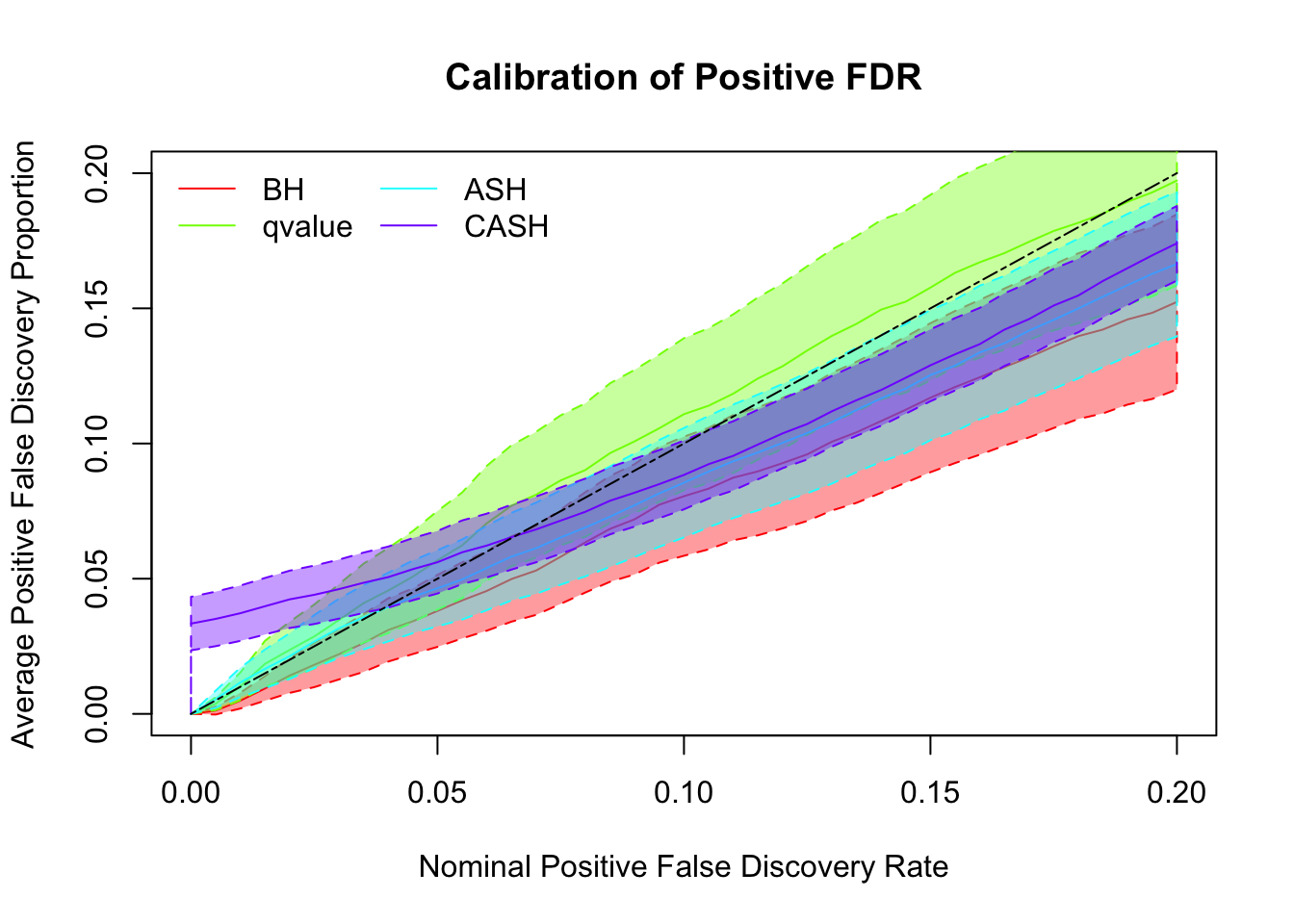
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
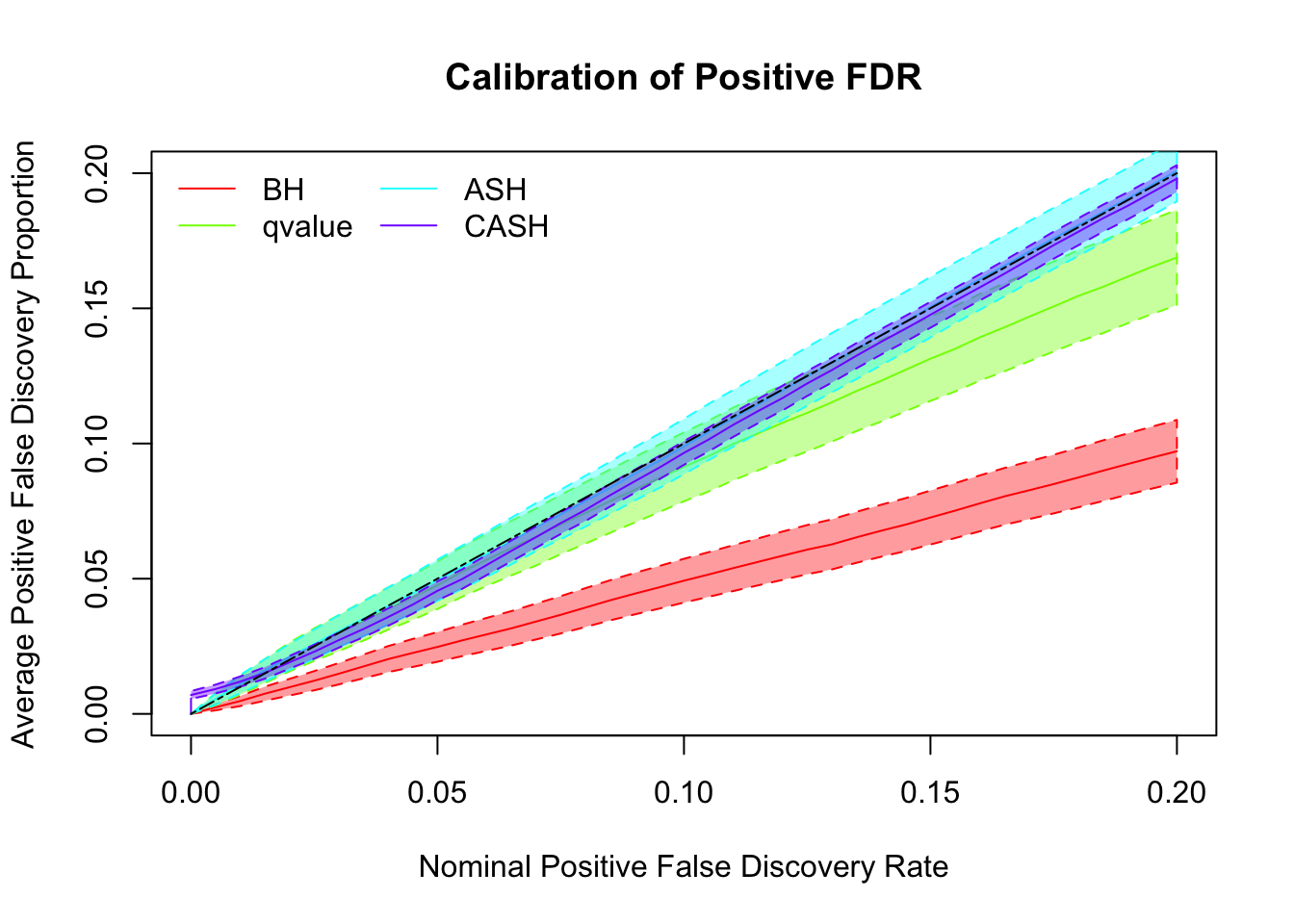
        g.pi = c(0.5, 0.5), g.sd = c(0, 1), relative_to_noise = FALSE)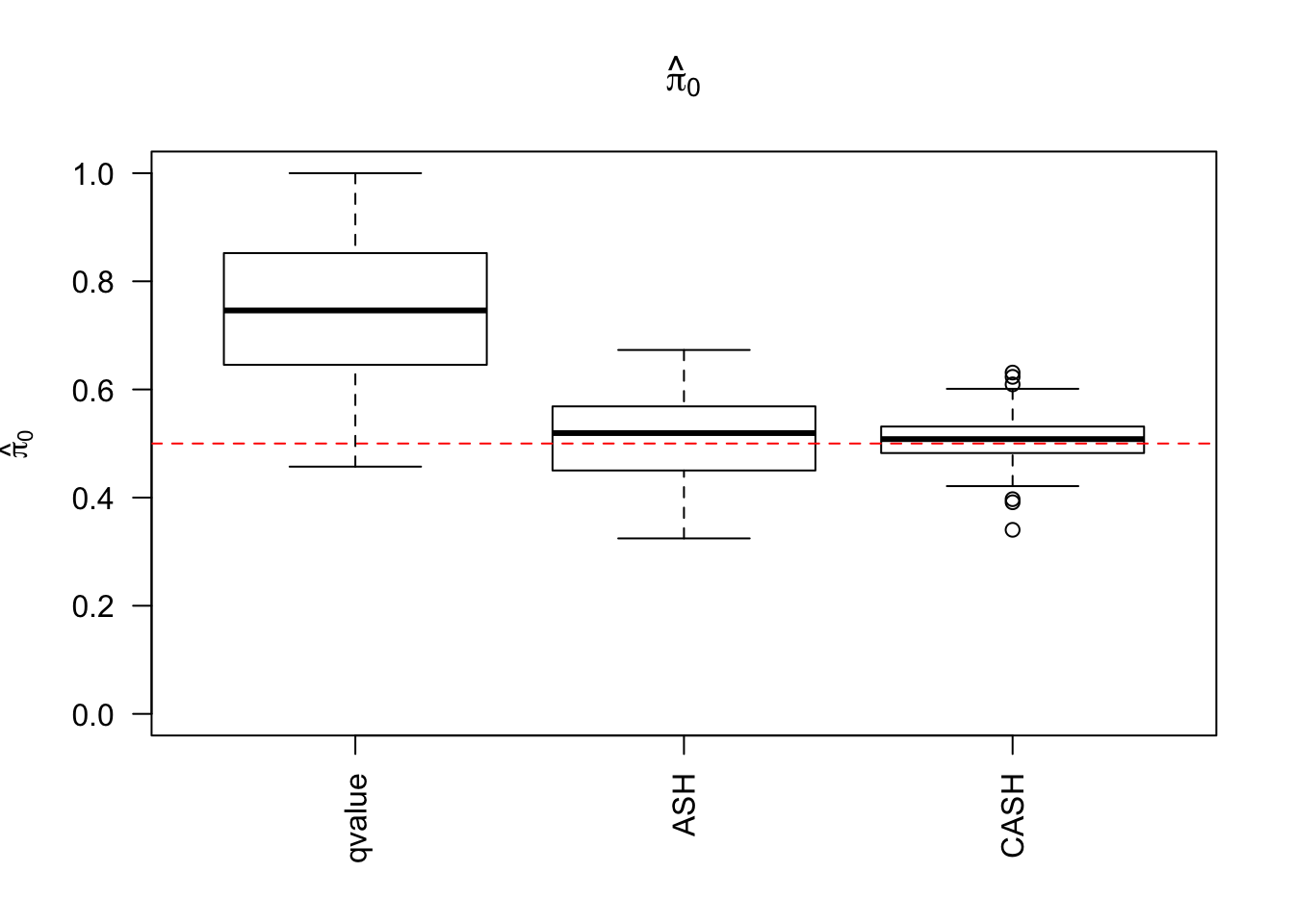

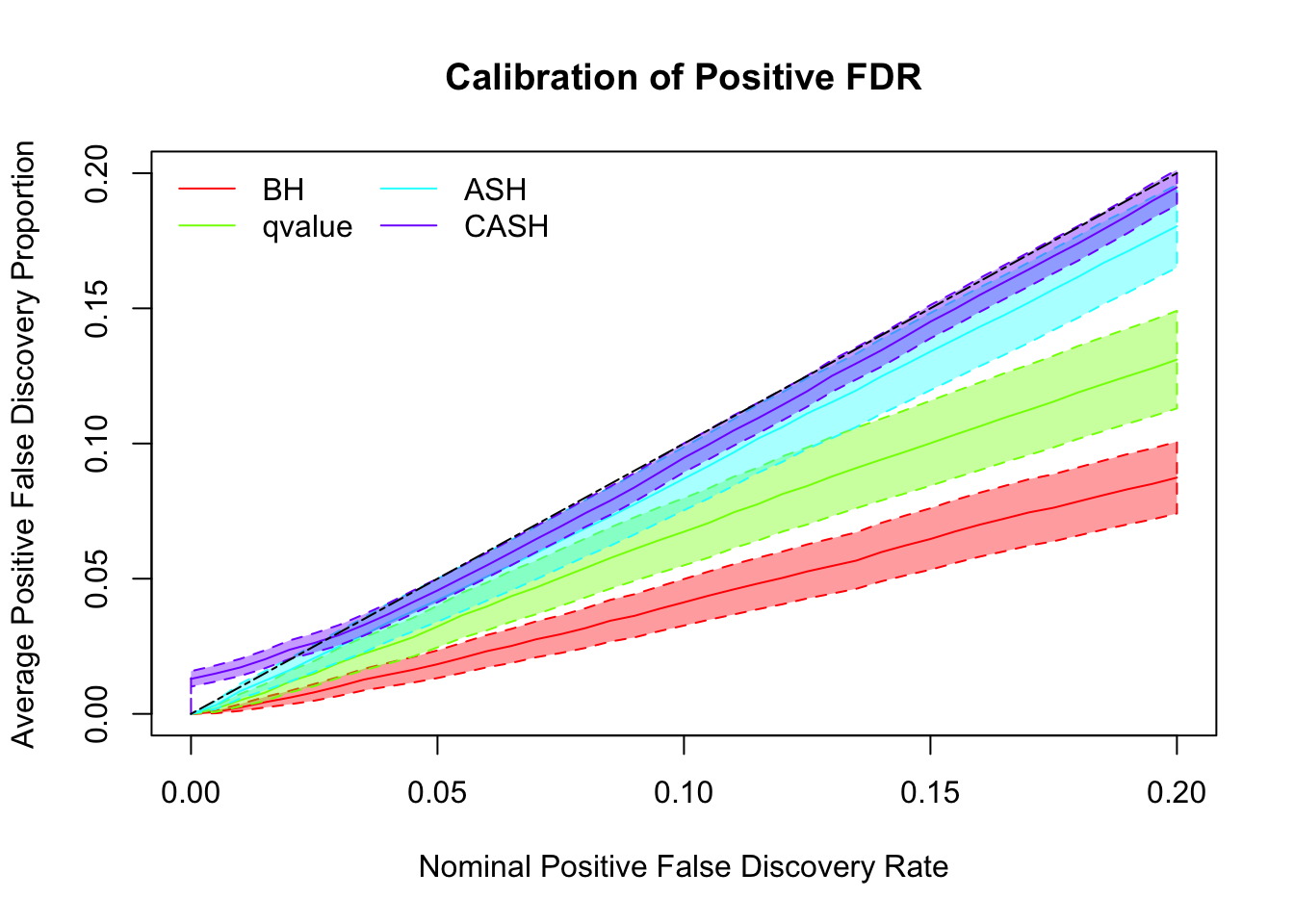
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.5, 0.5), g.sd = c(0, 2), relative_to_noise = FALSE)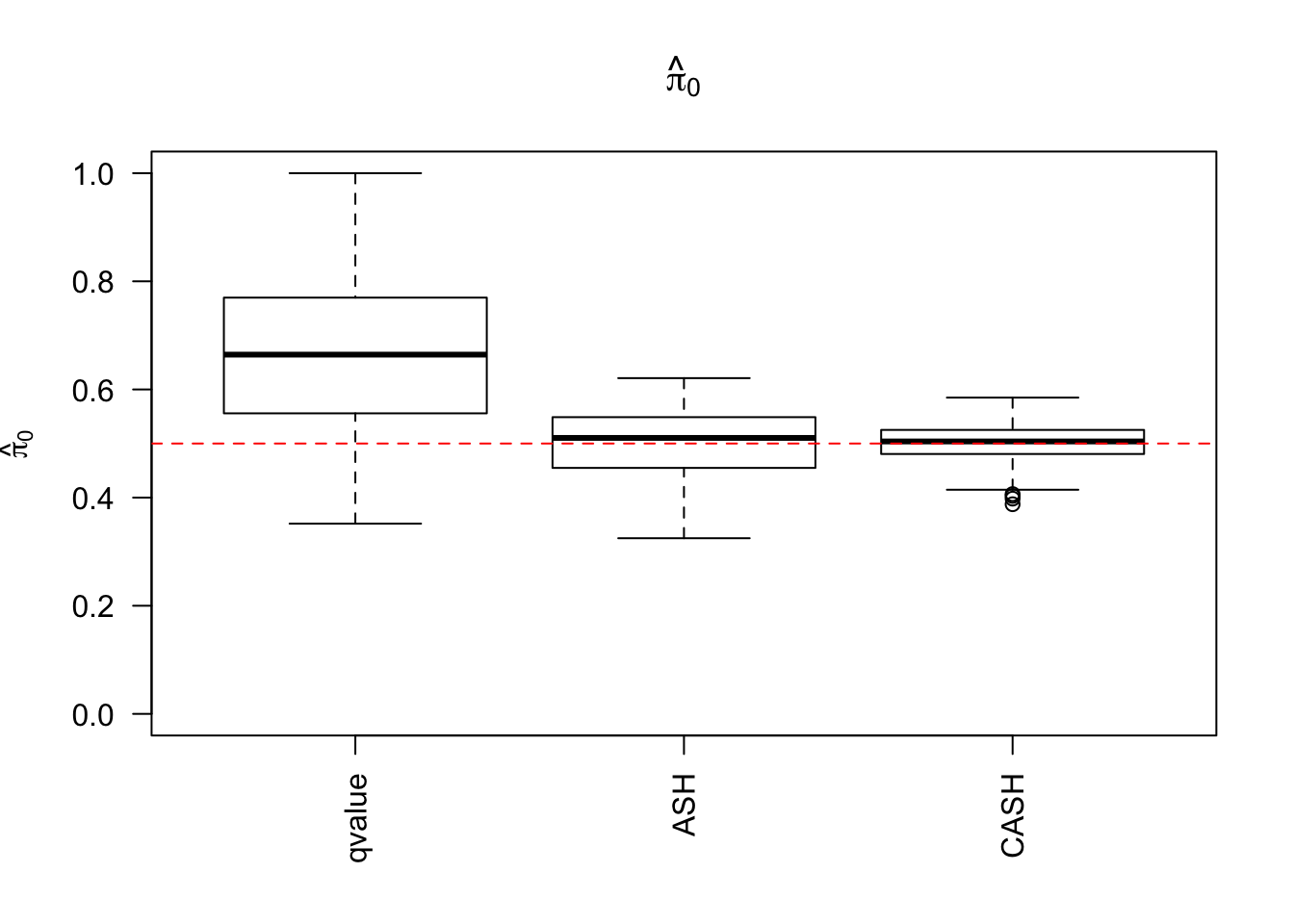

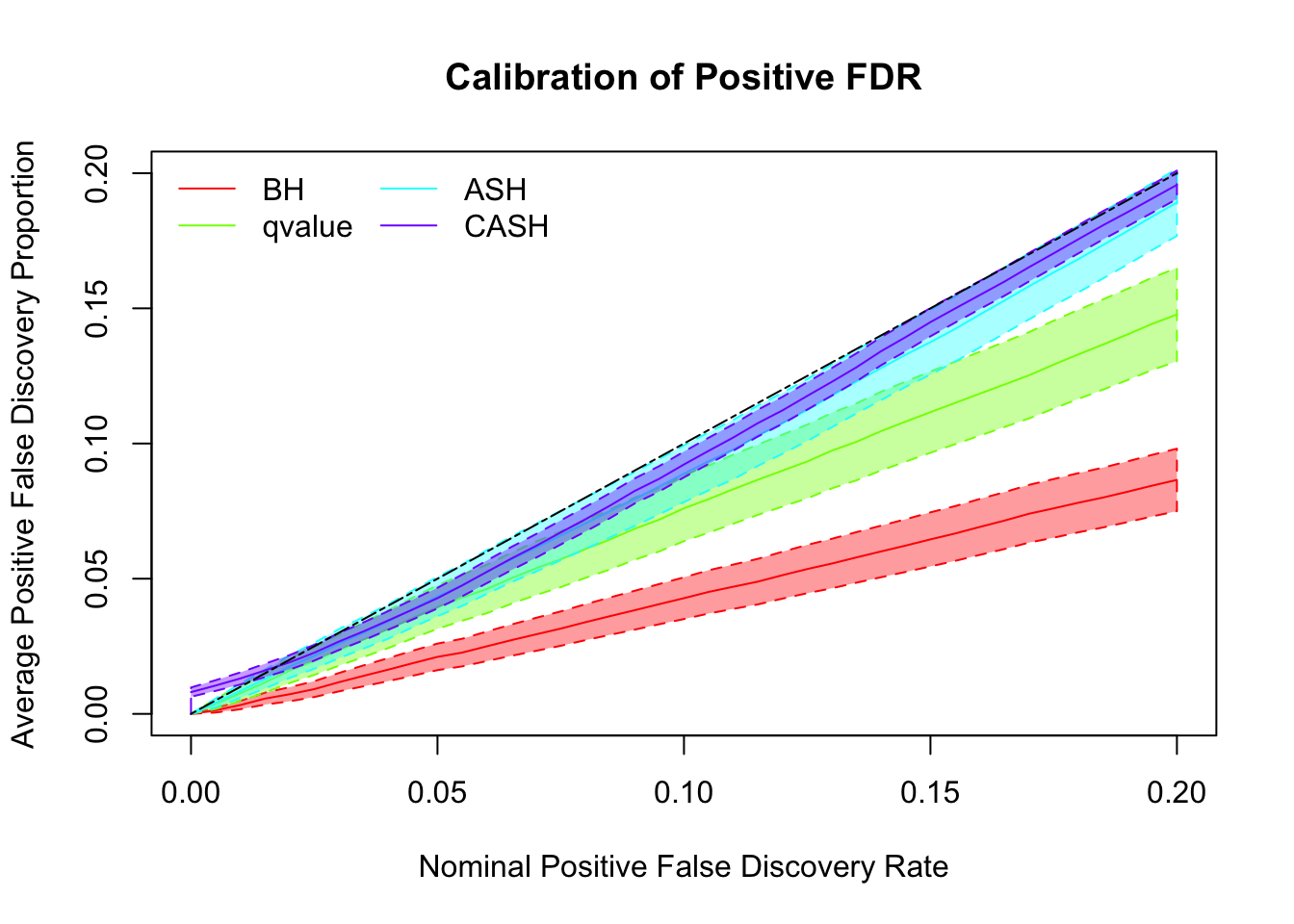
Simulation

cashSim(z.mat, se.mat,
        nsim = 200, ngene = 1000,
        g.pi = c(0.5, 0.5), g.sd = c(0, 3), relative_to_noise = FALSE)
Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol

Warning in REBayes::KWDual(A, rep(1, k), normalize(w), control = control): estimated mixing distribution has some negative values:
               consider reducing rtol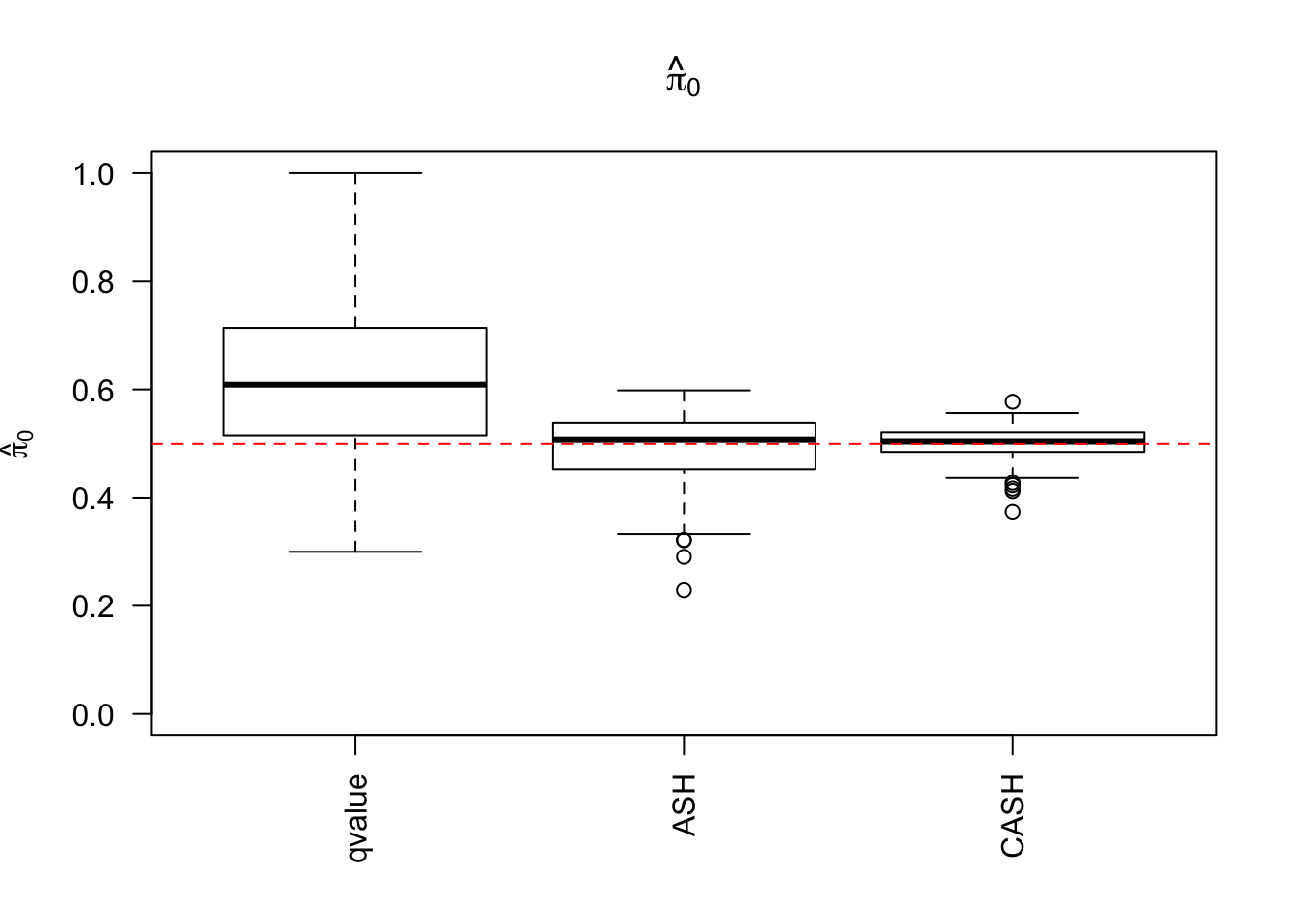

Read data

z.real <- readRDS("../output/z_null_liver_777.rds")
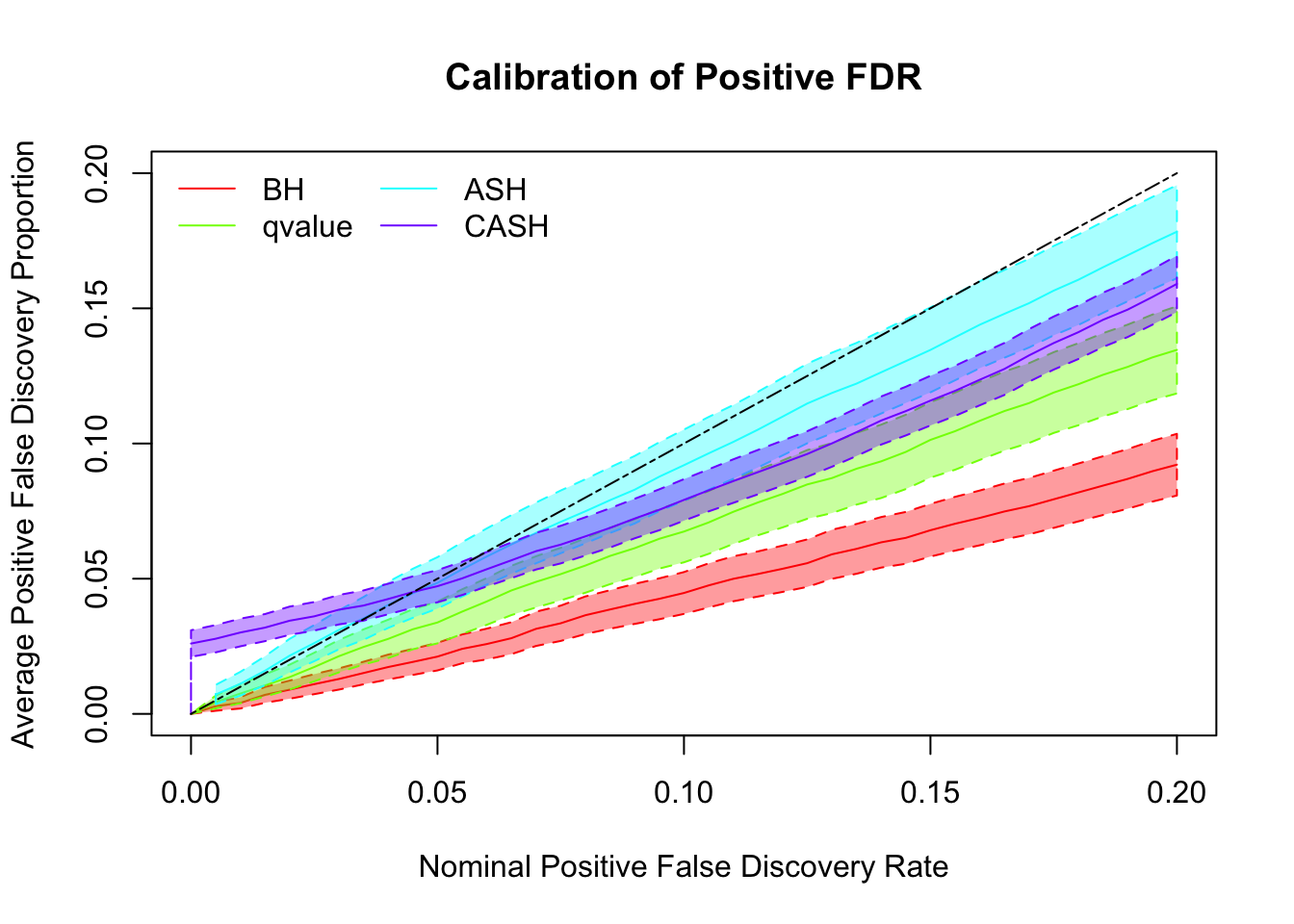
se.real <- readRDS("../output/sebetahat_null_liver_777.rds")

Simulation

cashSim(z.real, se.real,
        nsim = 200, ngene = 1000,
        g.pi = c(0.5, 0.5), g.sd = c(0, 1), relative_to_noise = TRUE)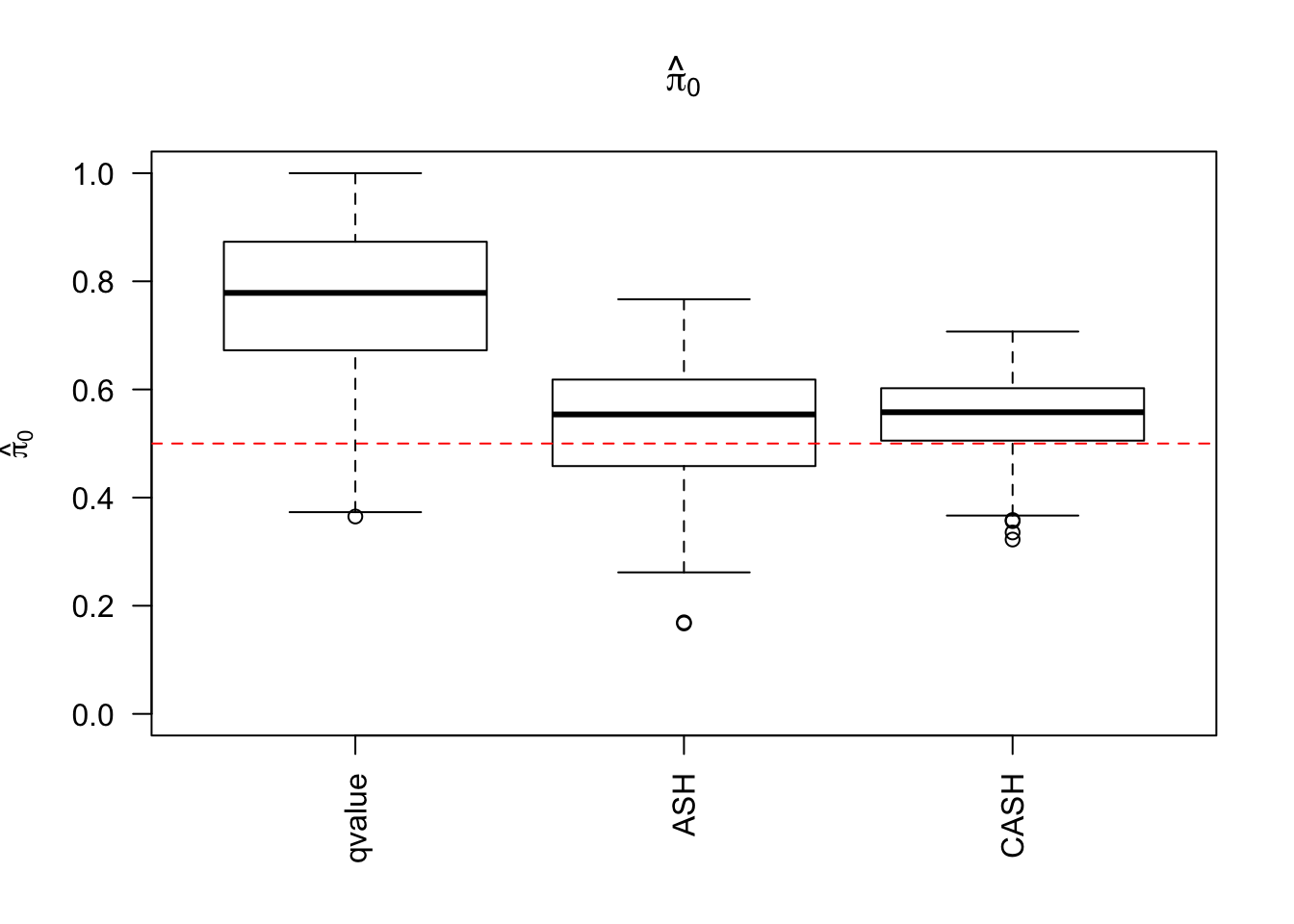

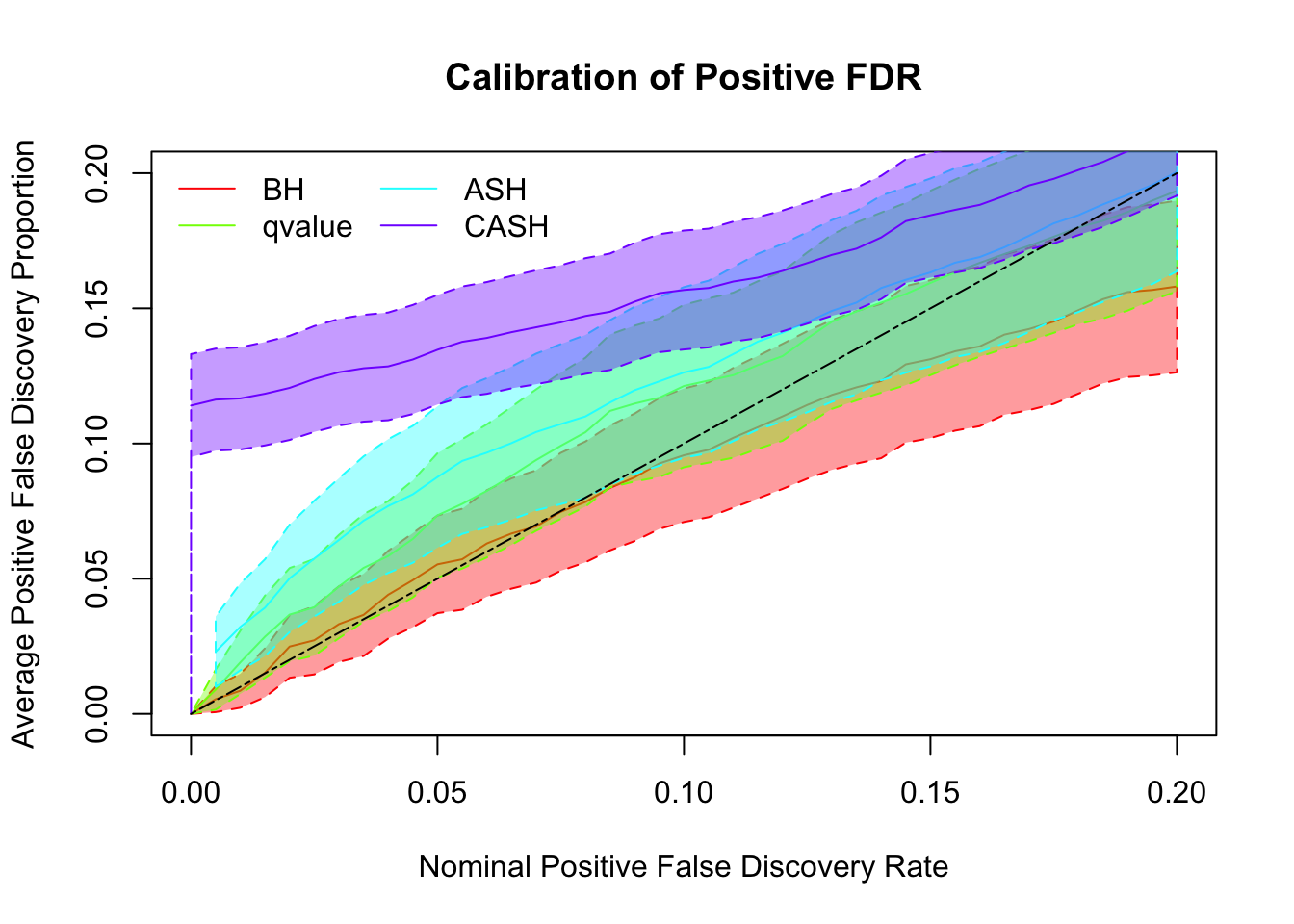
Simulation

cashSim(z.real, se.real,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.1), g.sd = c(0, 1), relative_to_noise = TRUE)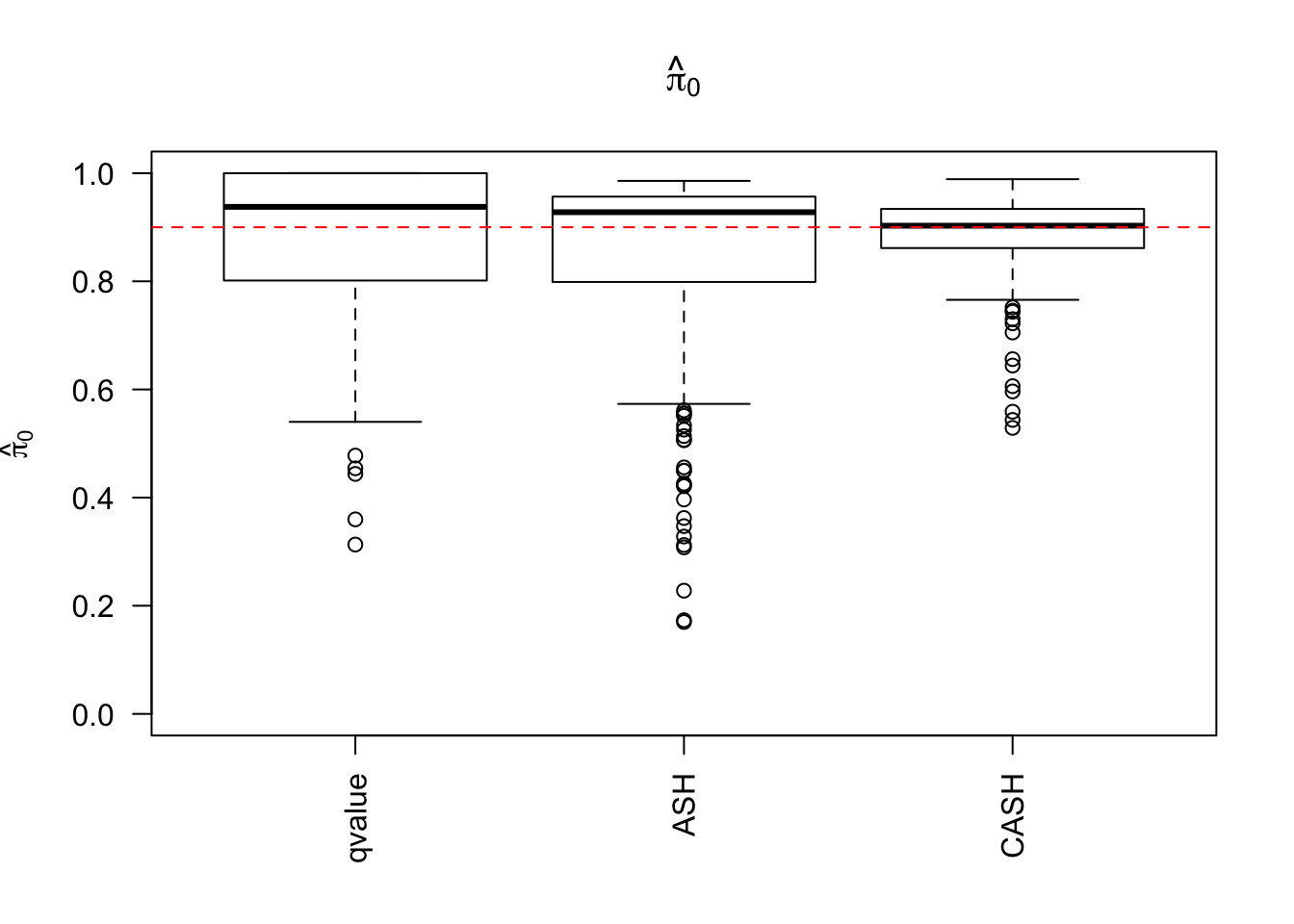

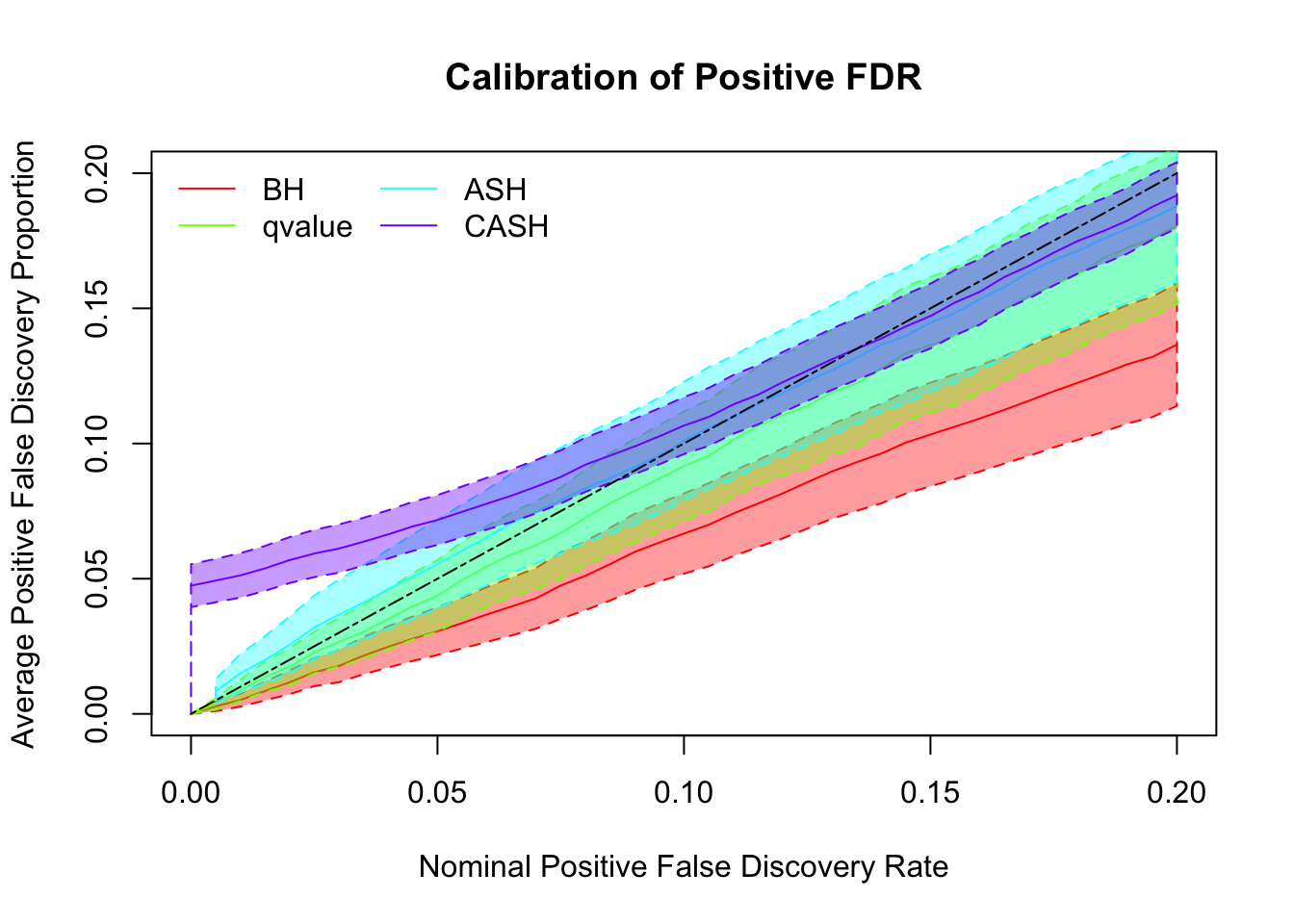
Simulation

cashSim(z.real, se.real,
        nsim = 200, ngene = 1000,
        g.pi = c(0.9, 0.1), g.sd = c(0, 2), relative_to_noise = TRUE)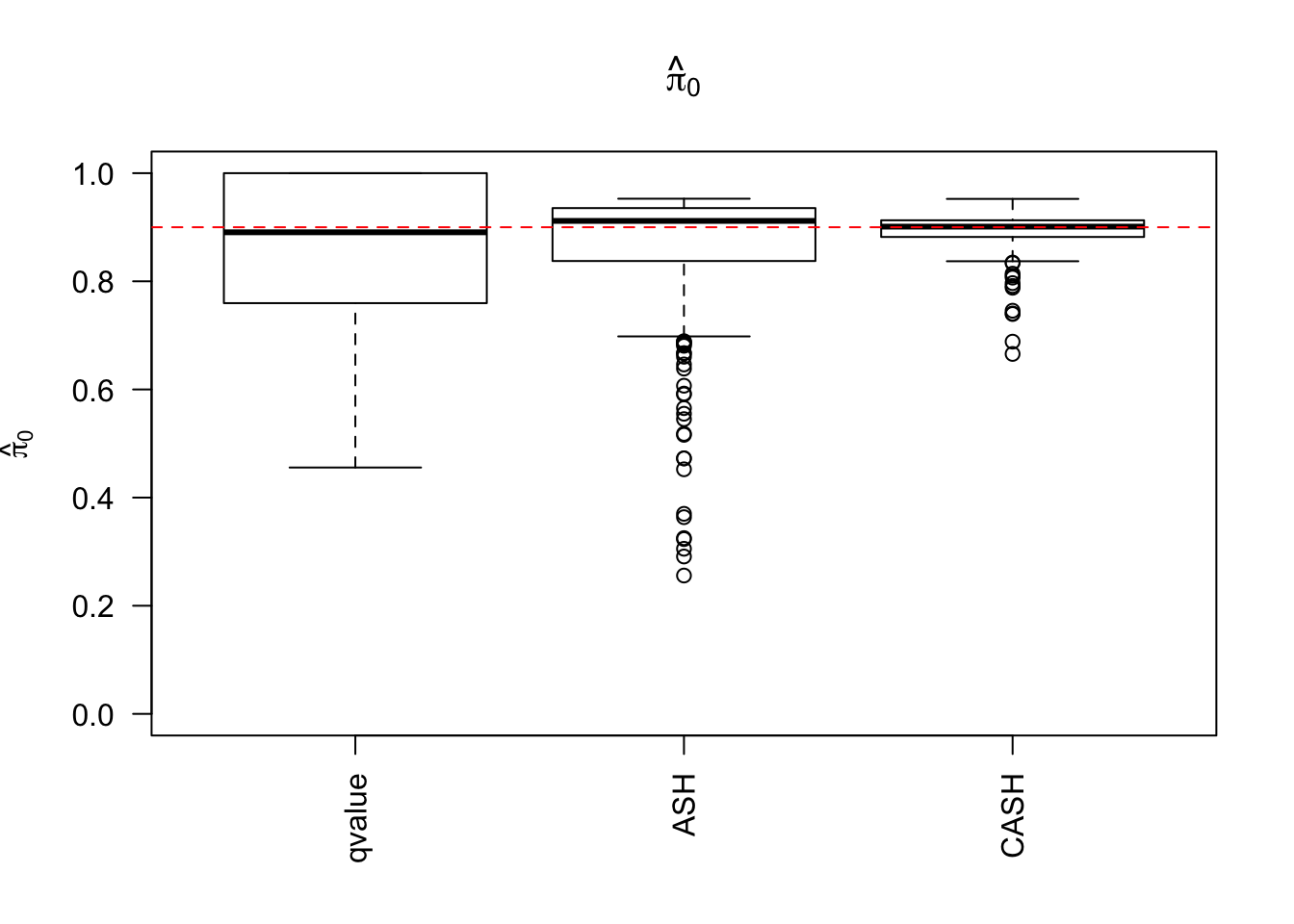

Session information

sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ashr_2.2-2        Rmosek_8.0.69     PolynomF_1.0-1    CVXR_0.94-4      
[5] REBayes_1.2       Matrix_1.2-12     SQUAREM_2017.10-1 EQL_1.0-0        
[9] ttutils_1.0-1    

loaded via a namespace (and not attached):
 [1] gmp_0.5-13.1      Rcpp_0.12.14      compiler_3.4.3   
 [4] git2r_0.20.0      R.methodsS3_1.7.1 R.utils_2.6.0    
 [7] iterators_1.0.9   tools_3.4.3       digest_0.6.13    
[10] bit_1.1-12        evaluate_0.10.1   lattice_0.20-35  
[13] foreach_1.4.4     yaml_2.1.16       parallel_3.4.3   
[16] Rmpfr_0.6-1       ECOSolveR_0.3-2   stringr_1.2.0    
[19] knitr_1.17        rprojroot_1.3-1   bit64_0.9-7      
[22] grid_3.4.3        R6_2.2.2          rmarkdown_1.8    
[25] magrittr_1.5      MASS_7.3-47       backports_1.1.2  
[28] codetools_0.2-15  htmltools_0.3.6   scs_1.1-1        
[31] stringi_1.1.6     doParallel_1.0.11 pscl_1.5.2       
[34] truncnorm_1.0-7   R.oo_1.21.0

This R Markdown site was created with workflowr