Last updated: 2017-12-21

Code version: 6e42447

Introduction

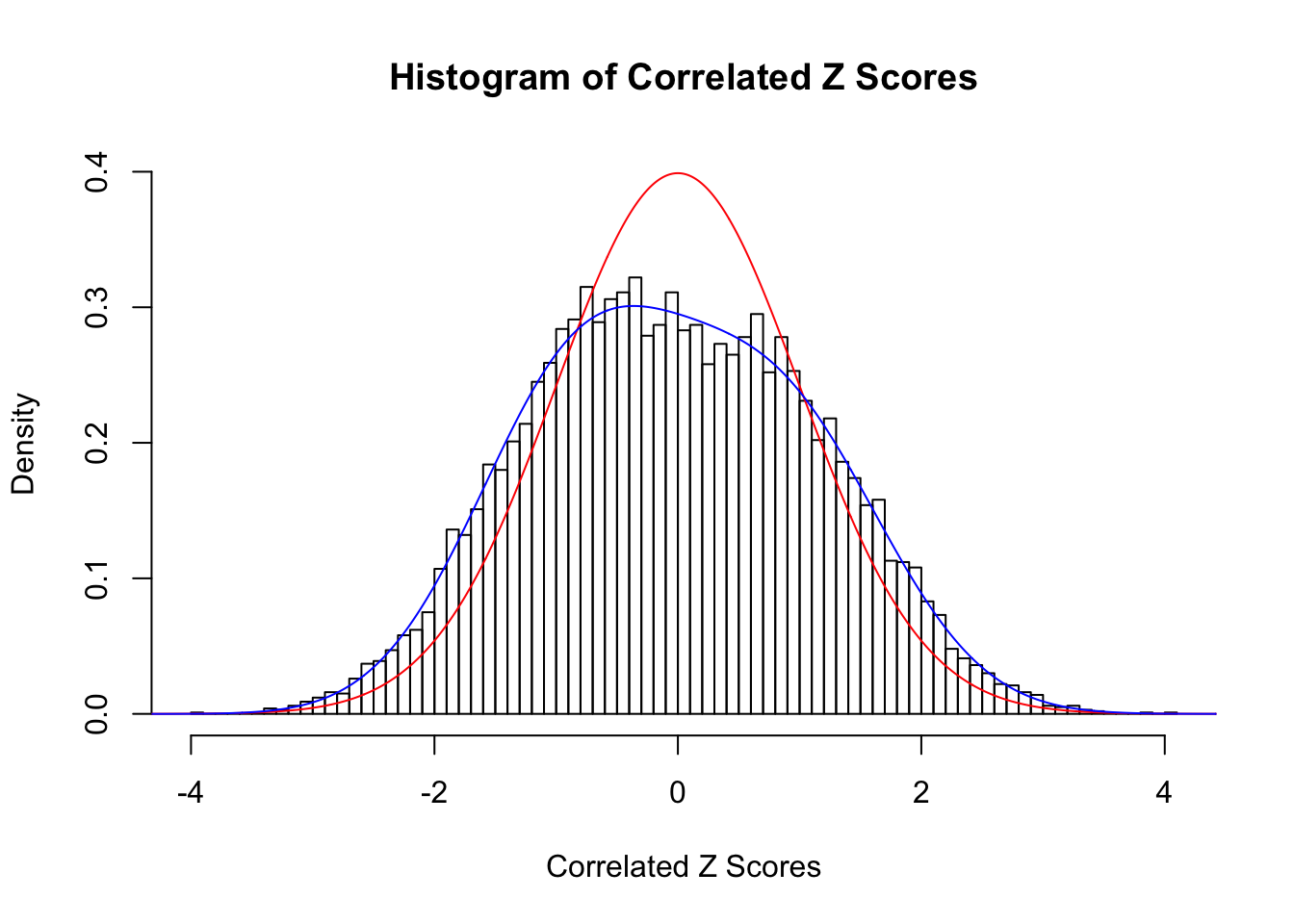
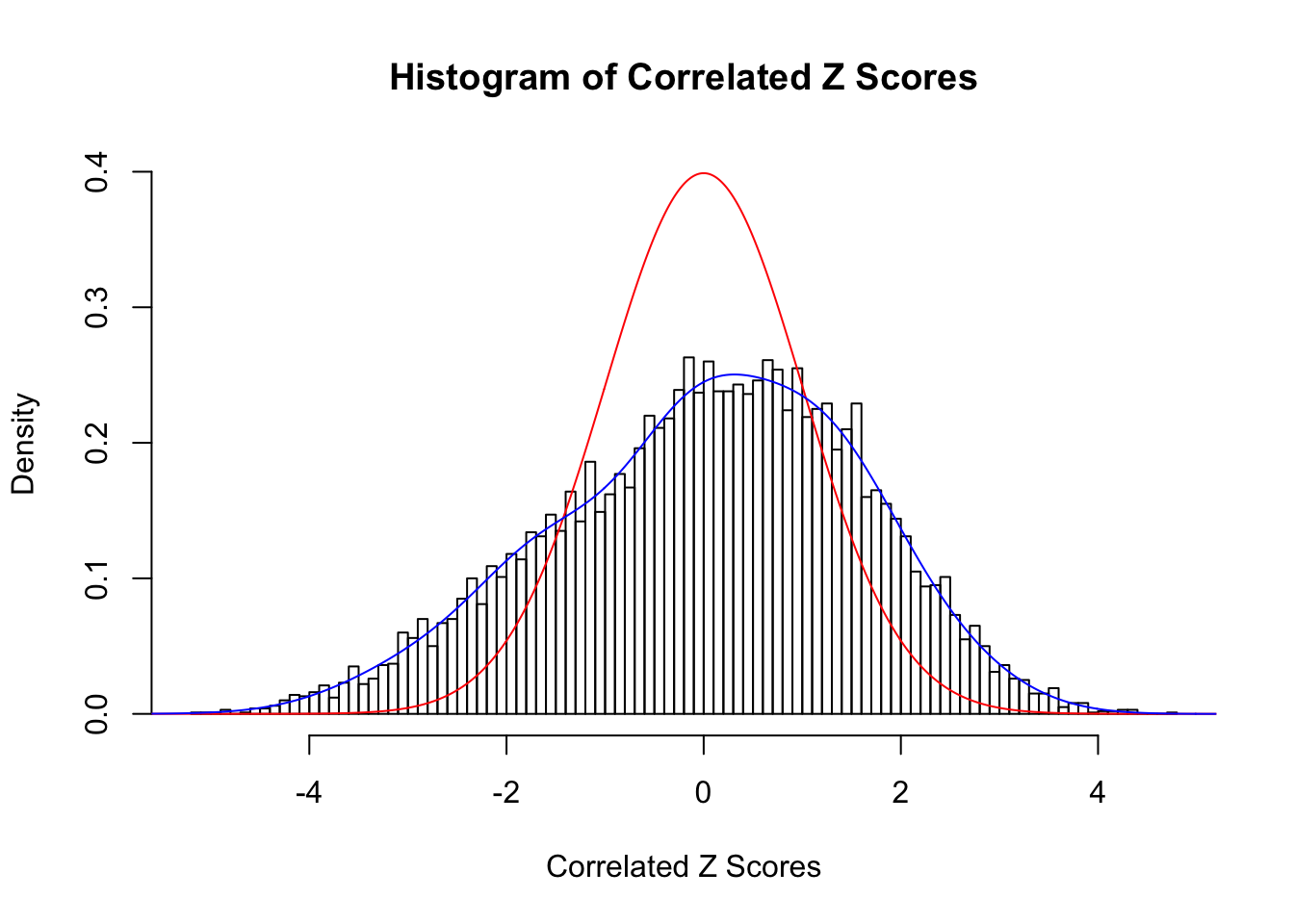
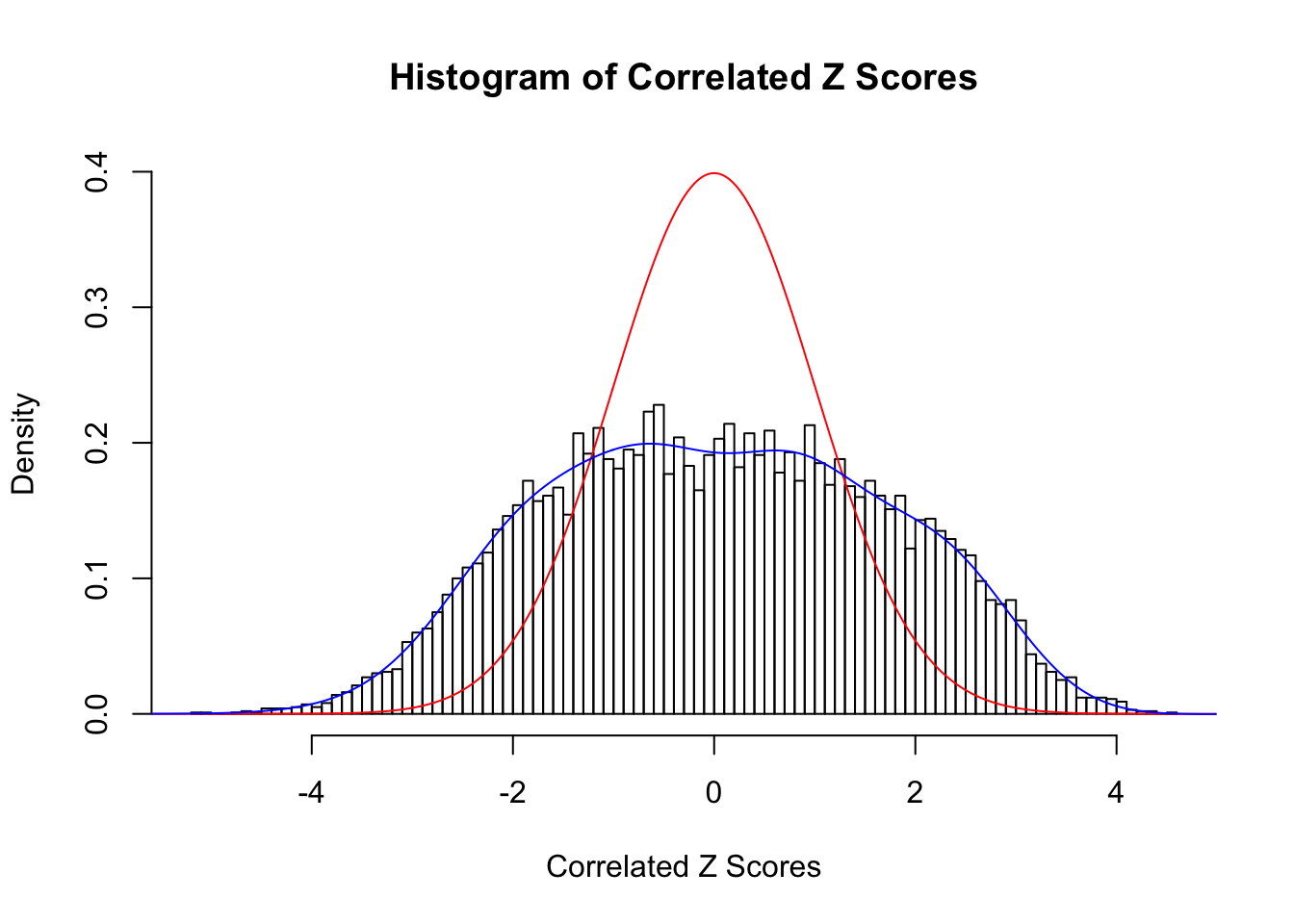
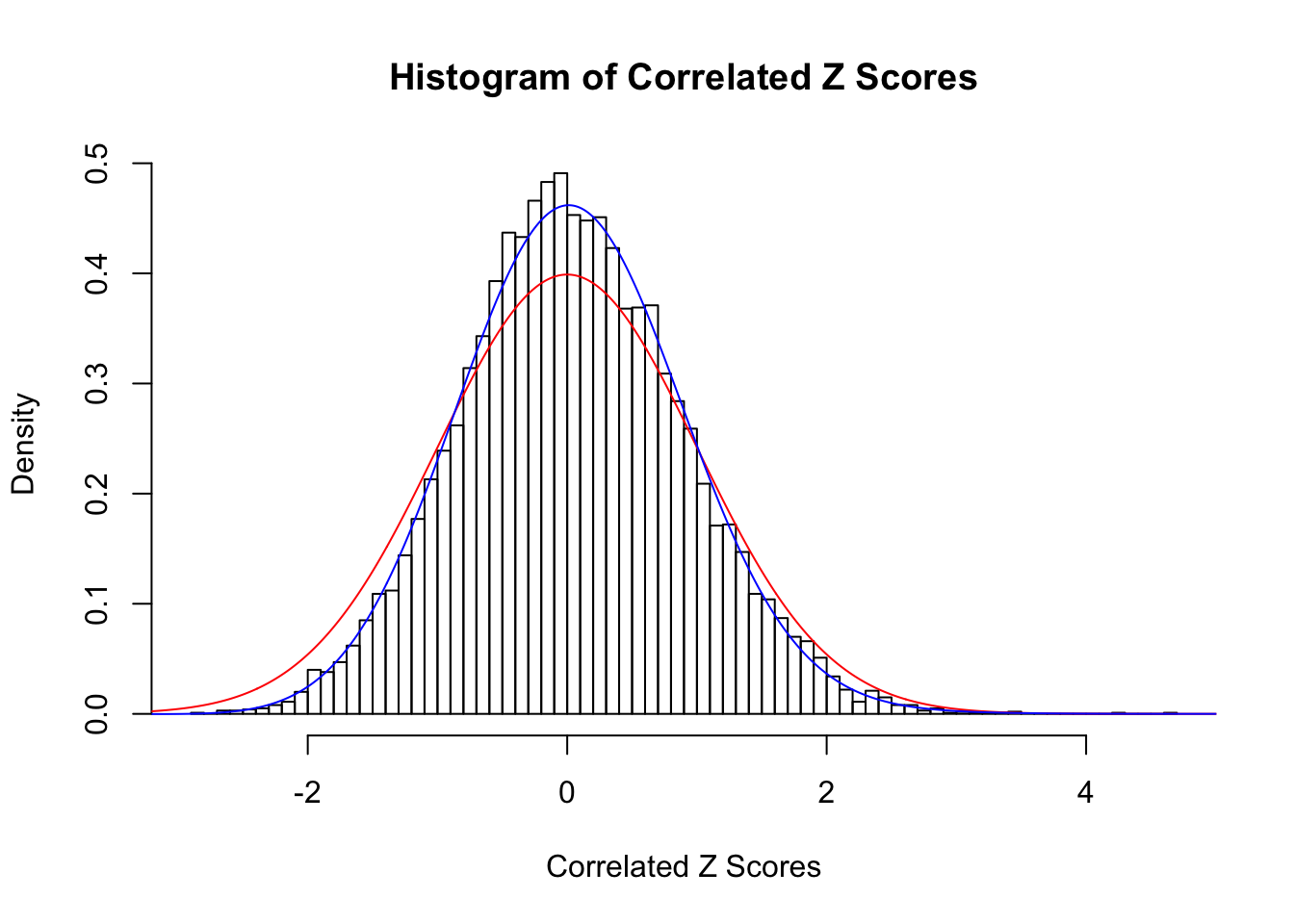
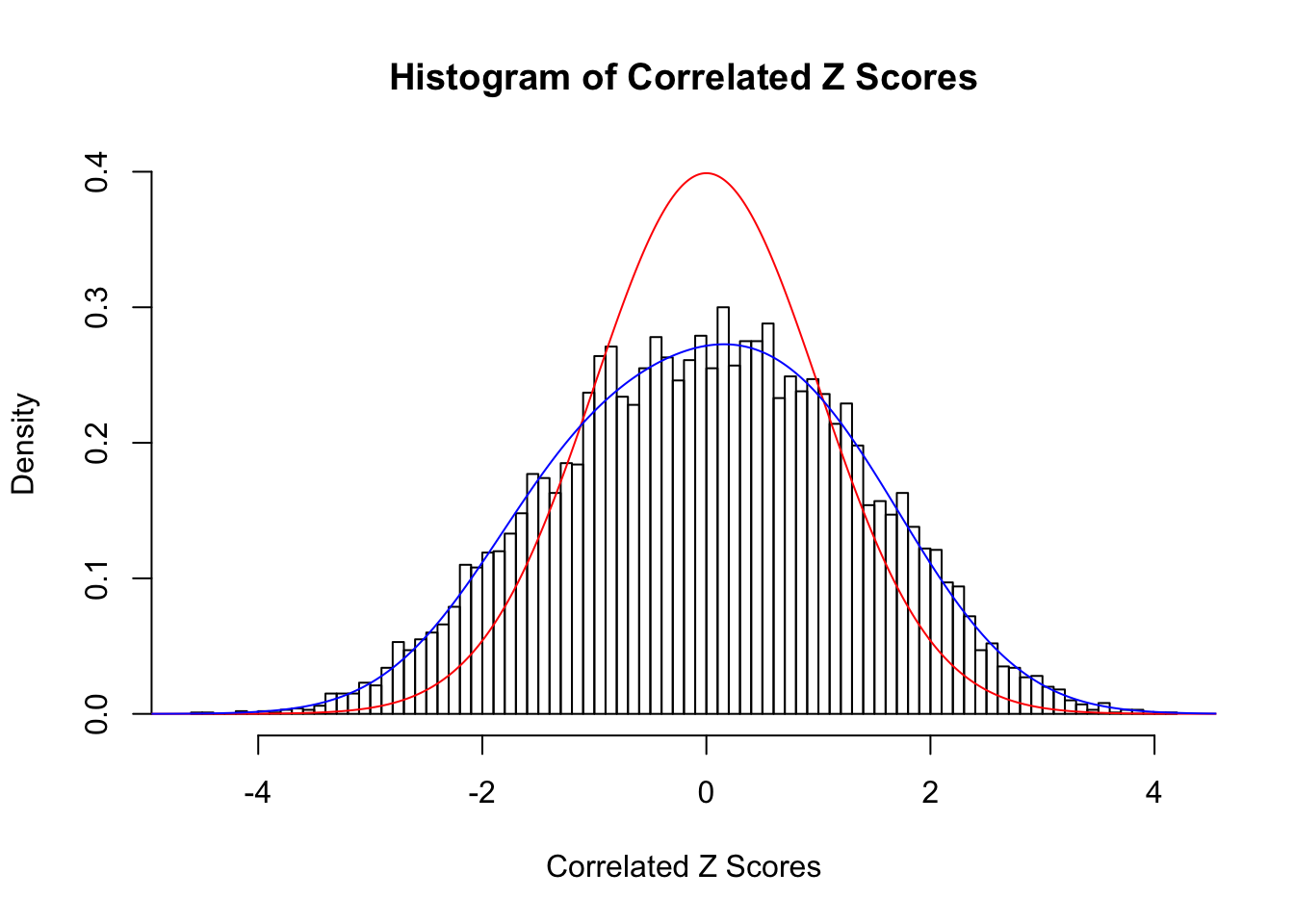
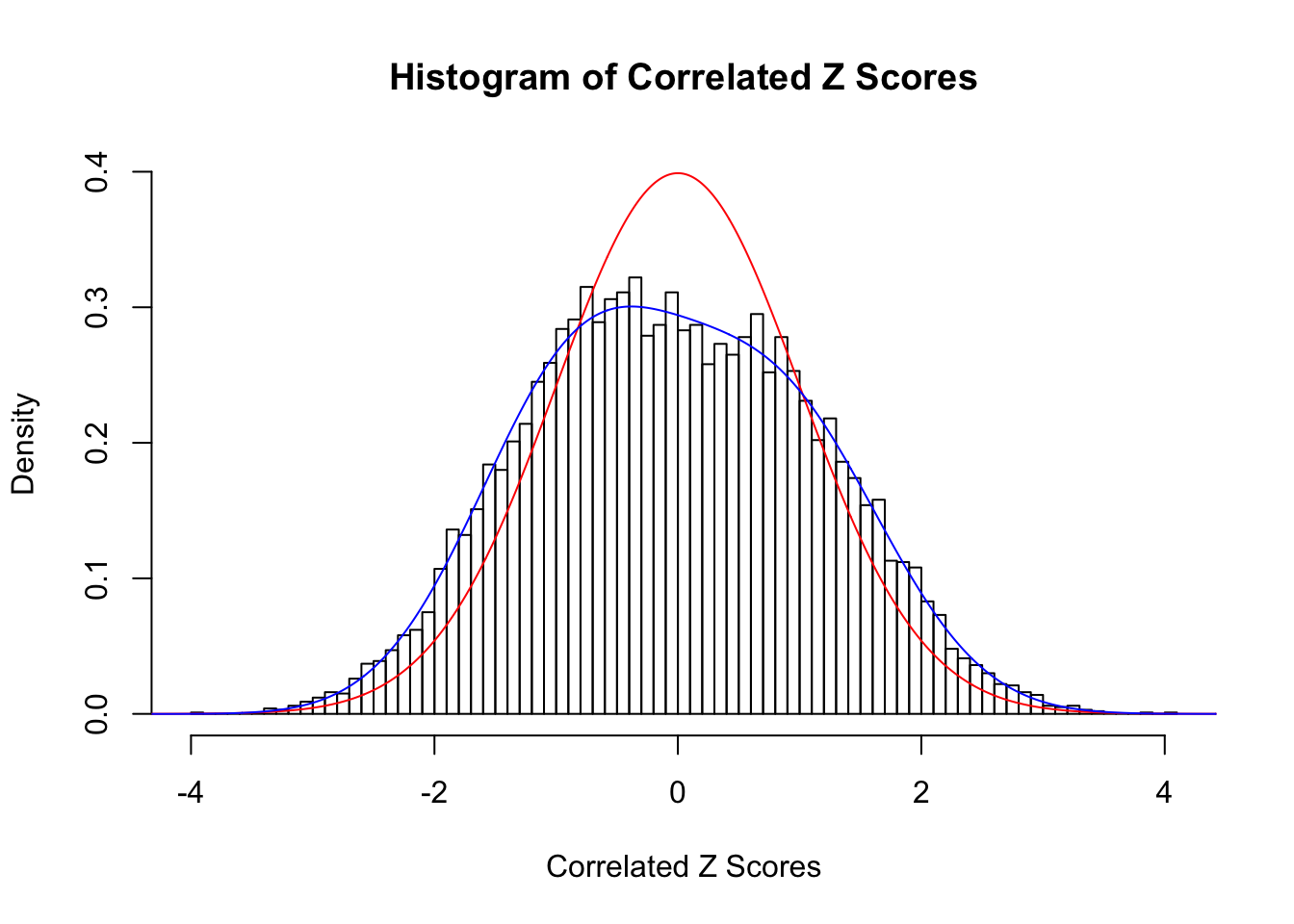
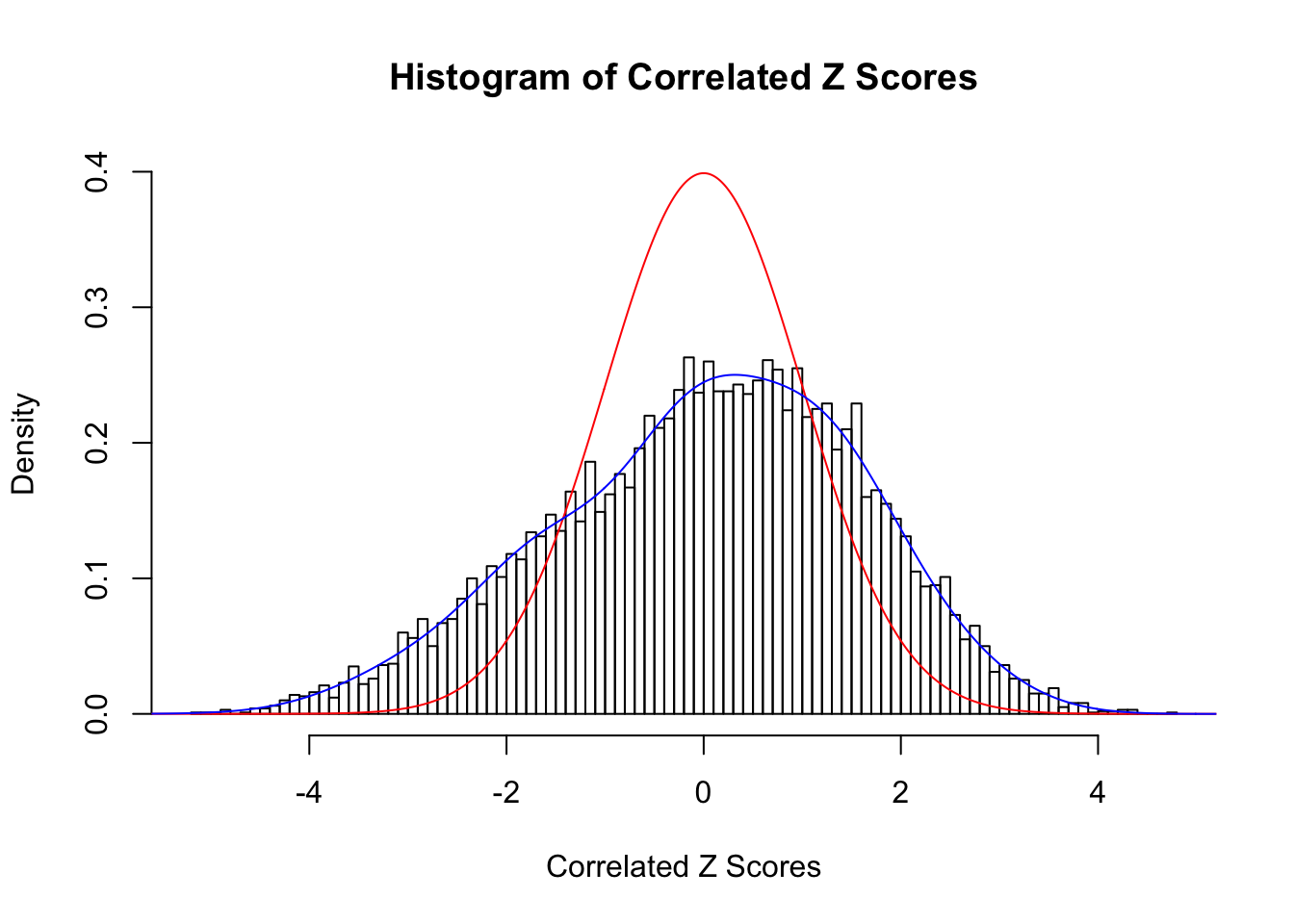
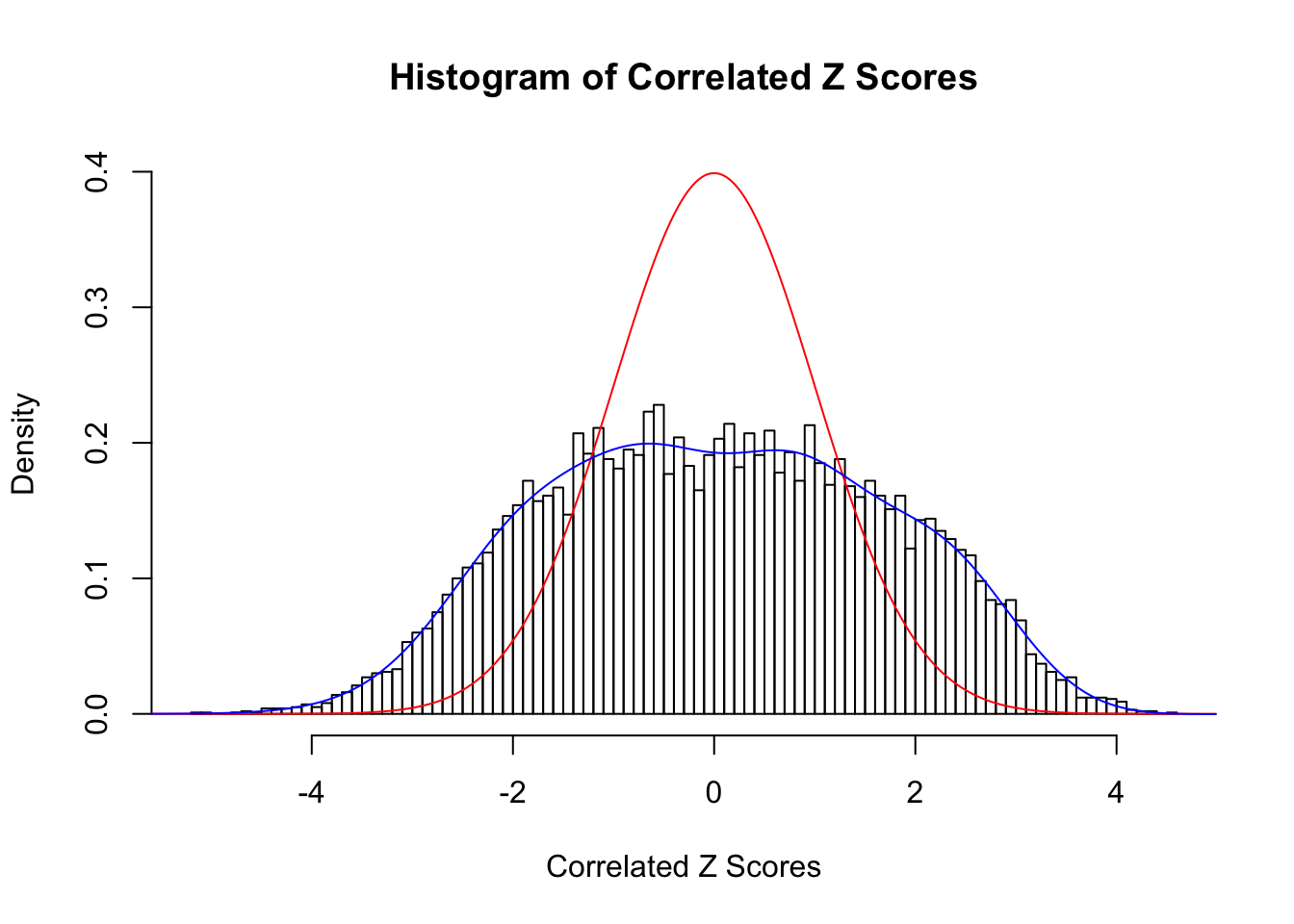
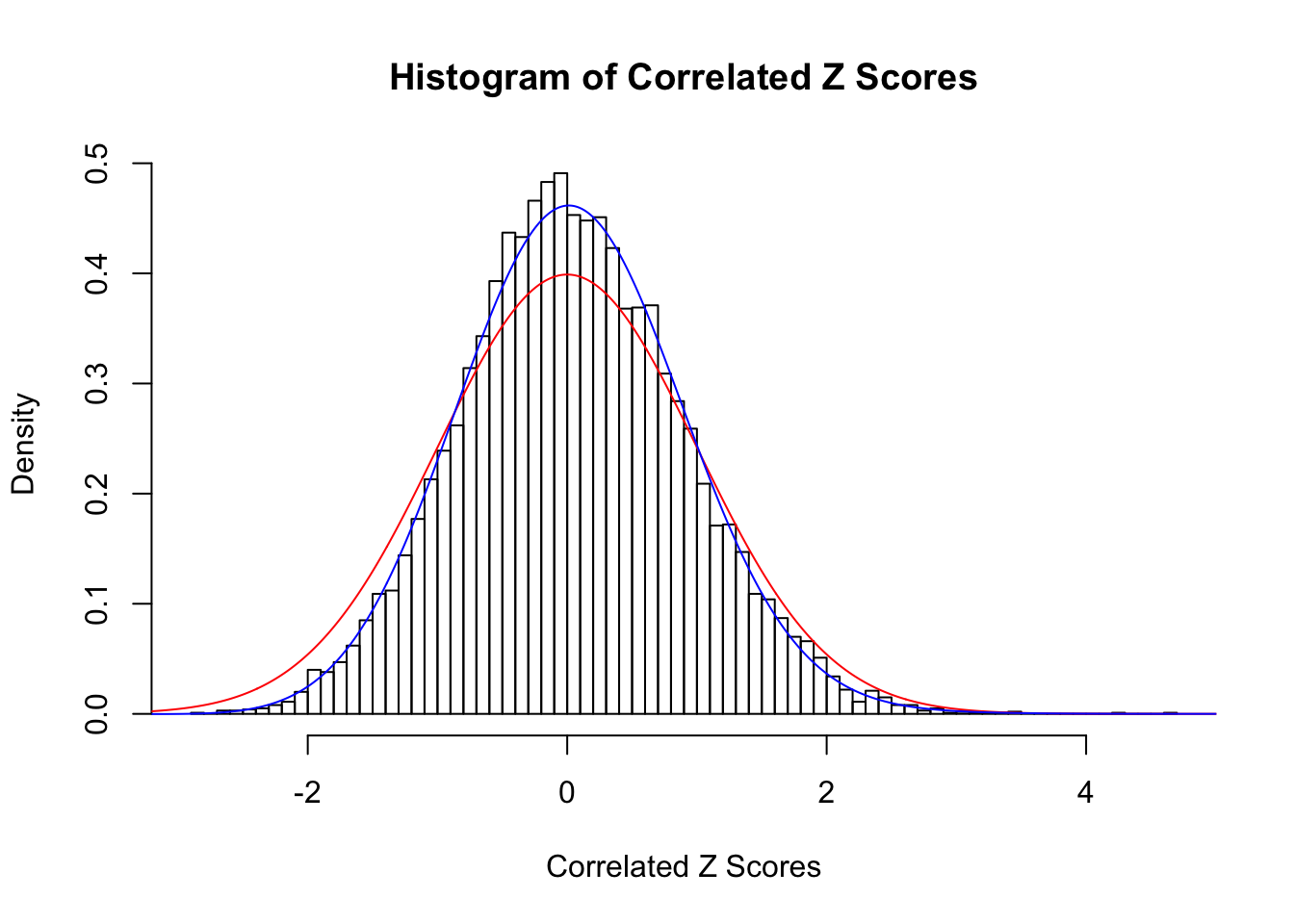
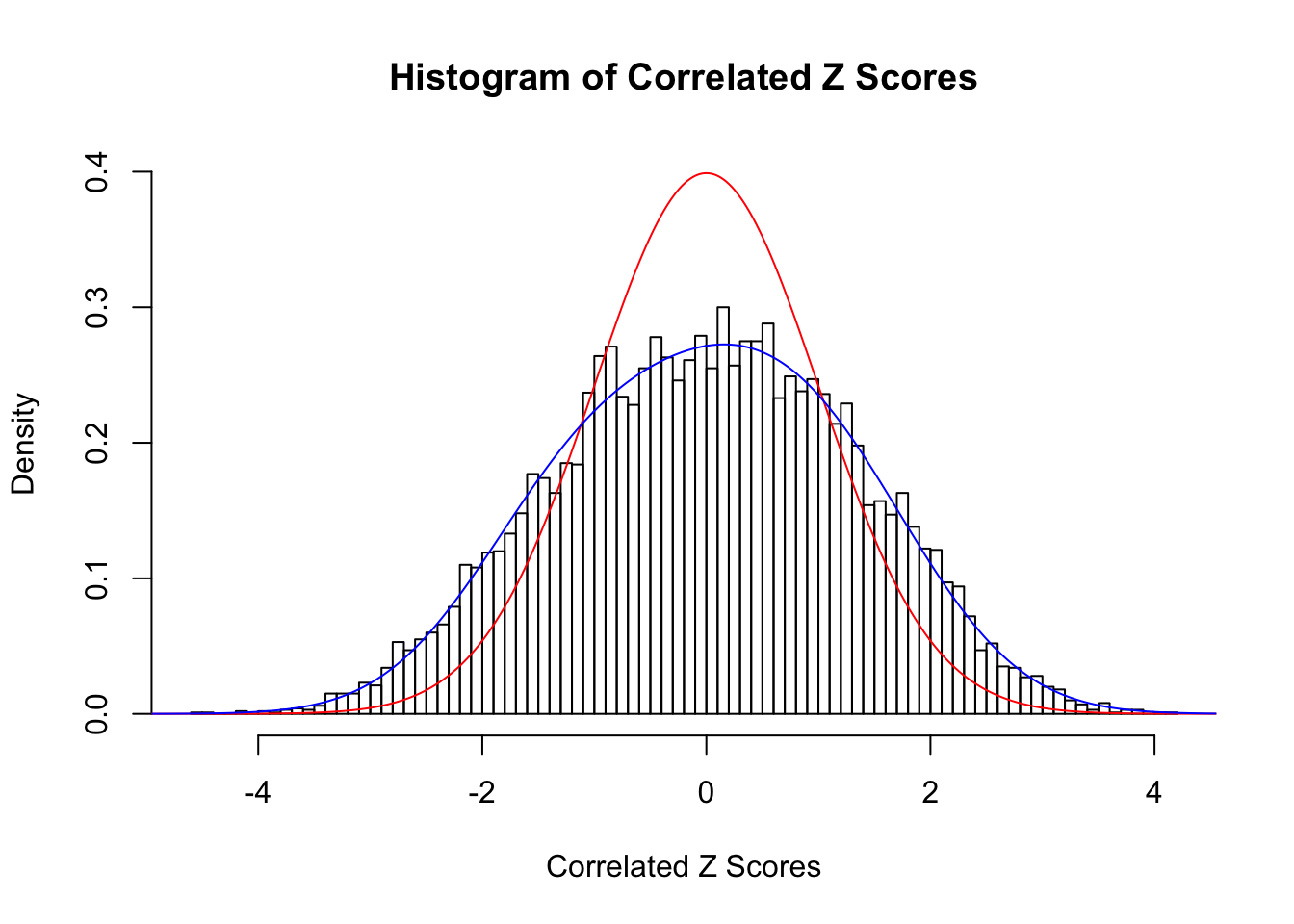
We are experimenting different ways to improve the performance of Rmosek, using typical data sets of correlated \(z\) scores.

z <- read.table("../output/z_null_liver_777.txt")
sel <- c(32, 327, 355, 483, 778)
ord <- c(4, 9, 9, 4, 4)
source("../code/gdash.R")

Algorithm and variations

Recall that our biconvex optimization problem is as follows.

\[ \begin{array}{rl} \min\limits_{\pi,w} & -\sum\limits_{j = 1}^n\log\left(\sum\limits_{k = 1}^K\sum\limits_{l=1}^L\pi_k w_l f_{jkl} + \sum\limits_{k = 1}^K\pi_kf_{jk0}\right) - \sum\limits_{k = 1}^K\left(\lambda_k^\pi - 1\right)\log\pi_k + \sum\limits_{l = 1}^L\lambda_l^w\phi\left(\left|w_l\right|\right) \\ \text{subject to} & \sum\limits_{k = 1}^K\pi_k = 1\\ & \sum\limits_{l=1}^L w_l \varphi^{(l)}\left(z\right) + \varphi\left(z\right) \geq 0, \forall z\in \mathbb{R}\\ & w_l \text{ decay reasonably fast,} \end{array} \] where \(- \sum\limits_{k = 1}^K\left(\lambda_k^\pi - 1\right)\log\pi_k\) and \(+ \sum\limits_{l = 1}^L\lambda_l^w\phi\left(\left|w_l\right|\right)\) are to regularize \(\pi_k\) and \(w_l\), respectively.

This problem can be solved iteratively. Starting with an initial value, each step two convex optimization problems are solved.

With a given \(\hat w\), \(\hat\pi\) is solved by

\[ \begin{array}{rl} \min\limits_{\pi} & -\sum\limits_{j = 1}^n\log\left(\sum\limits_{k = 1}^K\pi_k \left(\sum\limits_{l=1}^L \hat w_l f_{jkl} + f_{jk0}\right)\right) - \sum\limits_{k = 1}^K\left(\lambda_k^\pi - 1\right)\log\pi_k\\ \text{subject to} & \sum\limits_{k = 1}^K\pi_k = 1 \ ,\\ \end{array} \]

which is readily available with functions in cvxr.

Meanwhile, with a given \(\hat\pi\), the optimization problem to obtain \(\hat w\) becomes

\[ \begin{array}{rl} \min\limits_{w} & -\sum\limits_{j = 1}^n\log\left(\sum\limits_{l=1}^Lw_l\left(\sum\limits_{k = 1}^K\hat\pi_k f_{jkl}\right) + \sum\limits_{k = 1}^K\hat\pi_kf_{jk0}\right) + \sum\limits_{l = 1}^L\lambda_l^w \phi \left(\left|w_l\right|\right) \\ \text{subject to} & \sum\limits_{l=1}^L w_l \varphi^{(l)}\left(z\right) + \varphi\left(z\right) \geq 0, \forall z\in \mathbb{R}\\ & w_l \text{ decay reasonably fast.} \end{array} \] The two constraints are important to prevent numerical instability. Yet they are not readily manifested as convex. Ideally, the regularization \(\sum\limits_{l = 1}^L\lambda_l^w\phi\left(\left|w_l\right|\right)\) would be able to capture the essence of these two constaints, and at the same time maintain the convexity. Different ideas will be explored.

In this part, we’ll mainly work on the “basic form” of the \(w\) optimization problem; that is, the optimization problem without regularization \(\sum\limits_{l = 1}^L\lambda_l^w\phi\left(\left|w_l\right|\right)\).

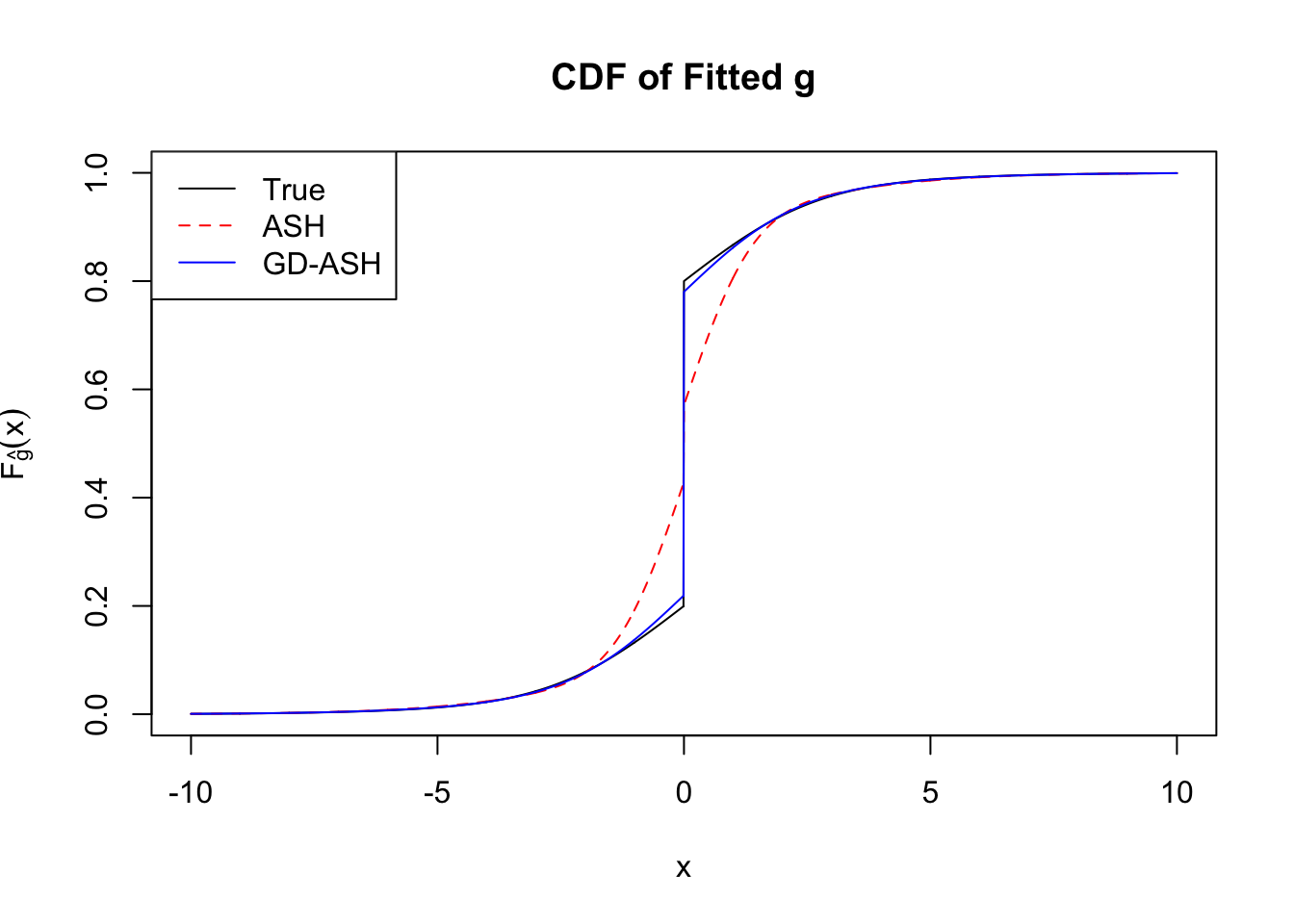
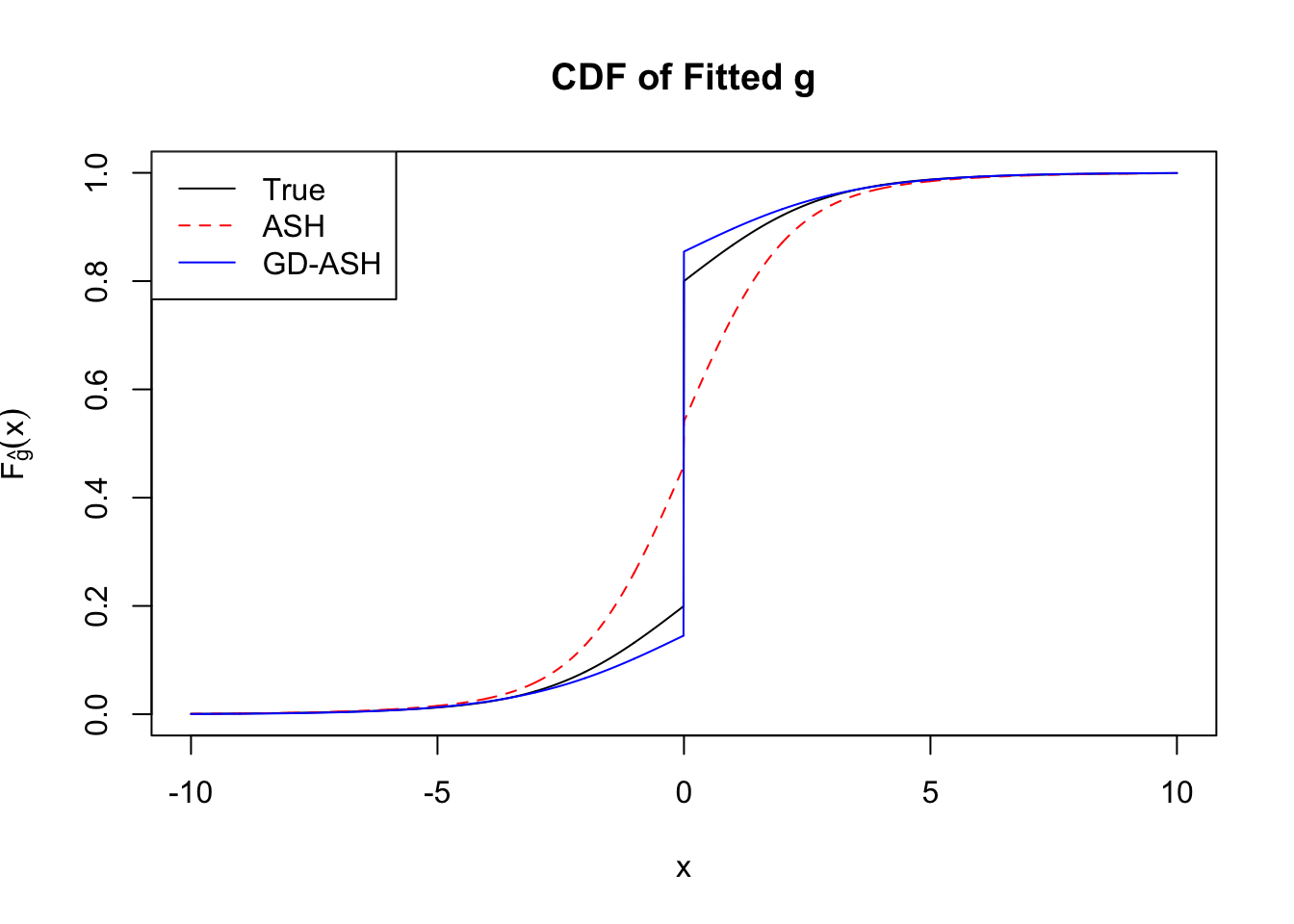
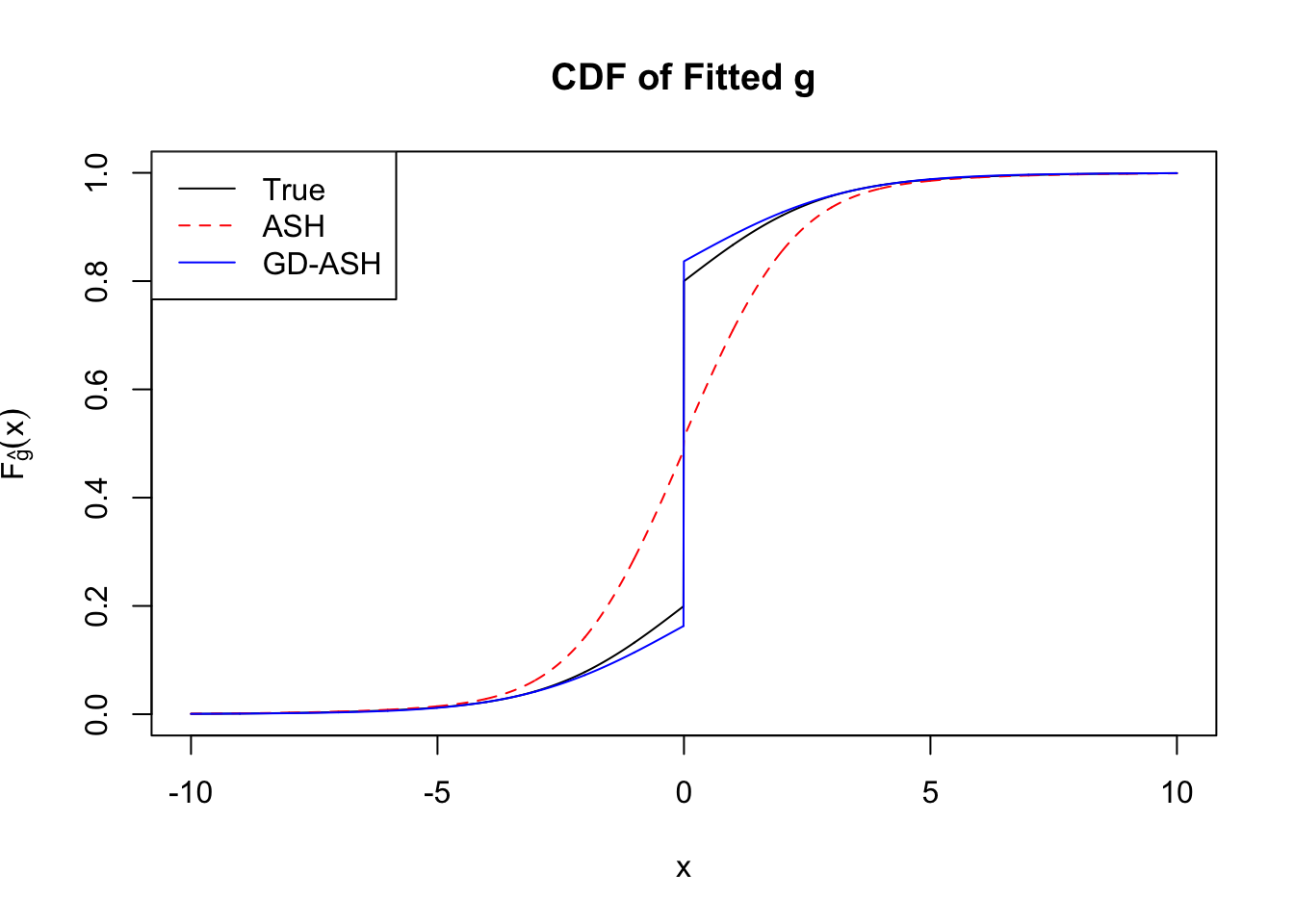
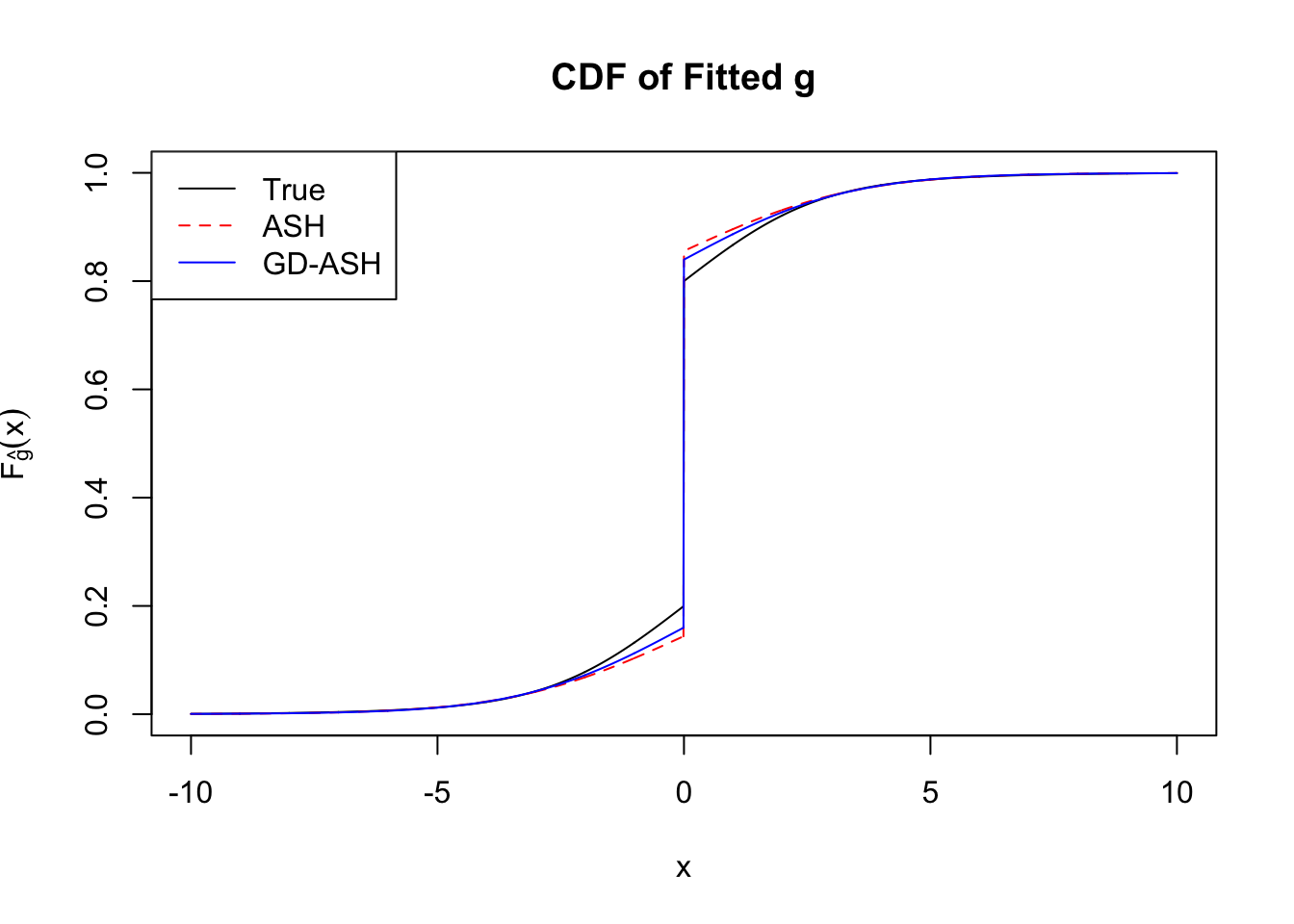
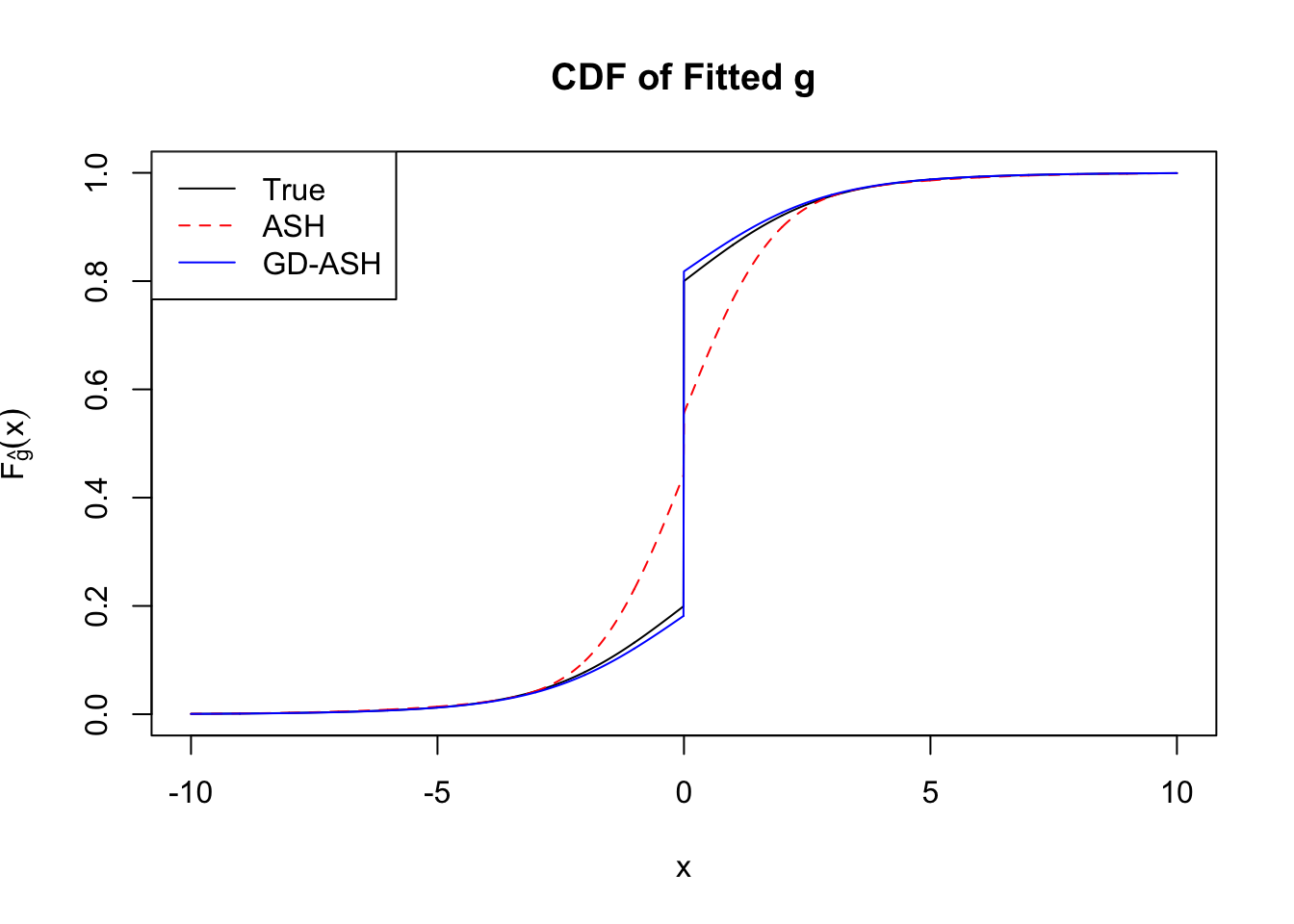
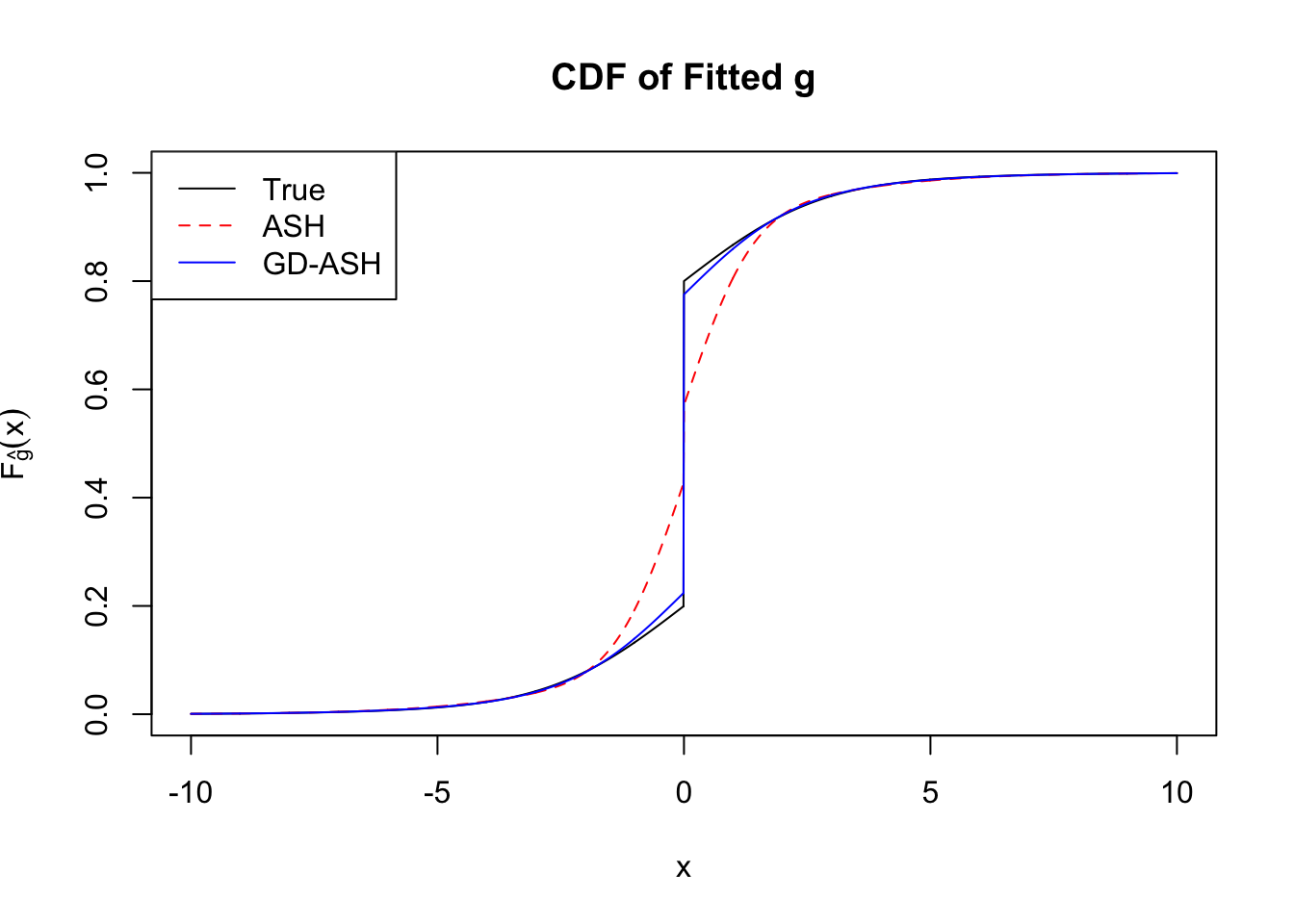
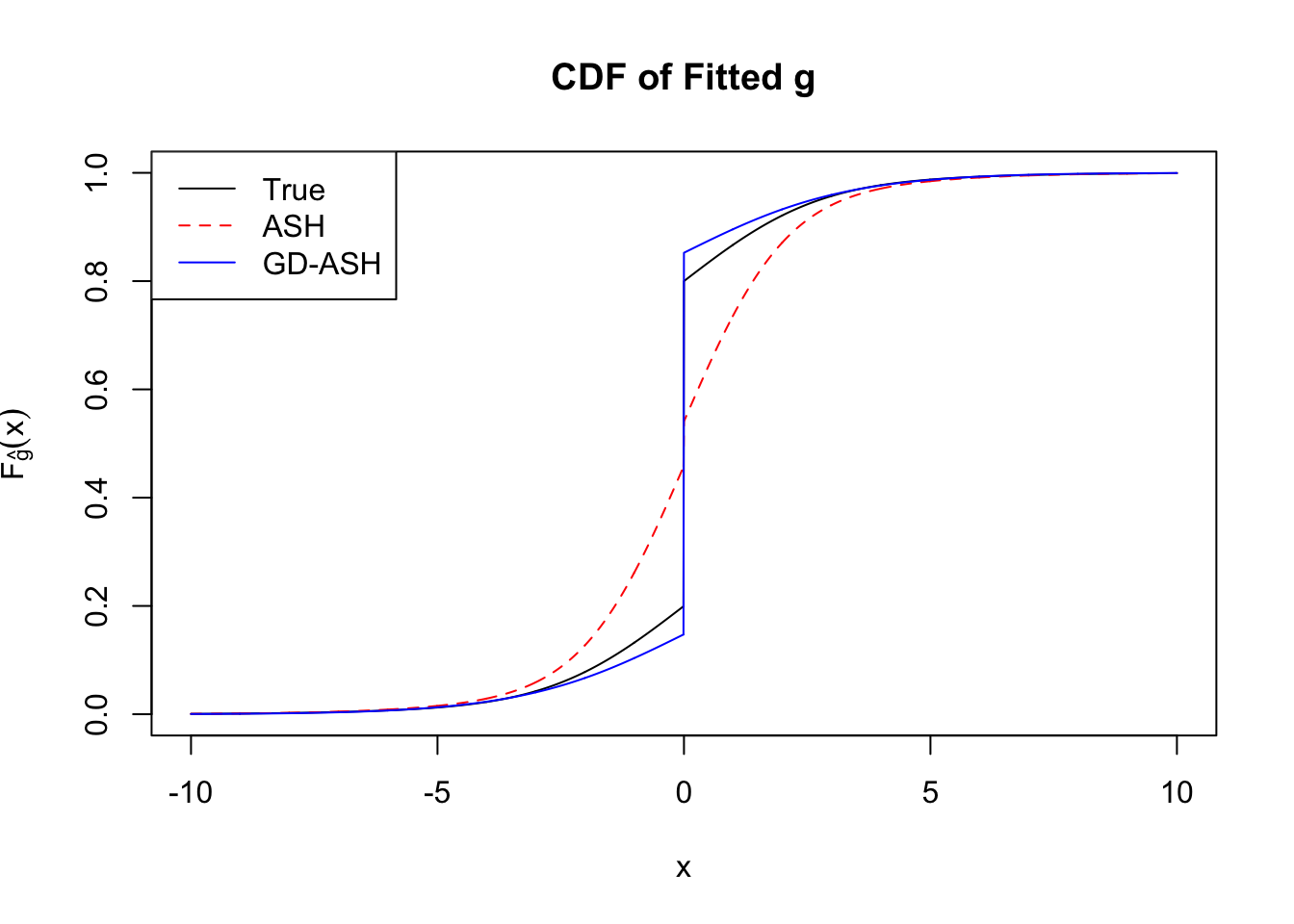
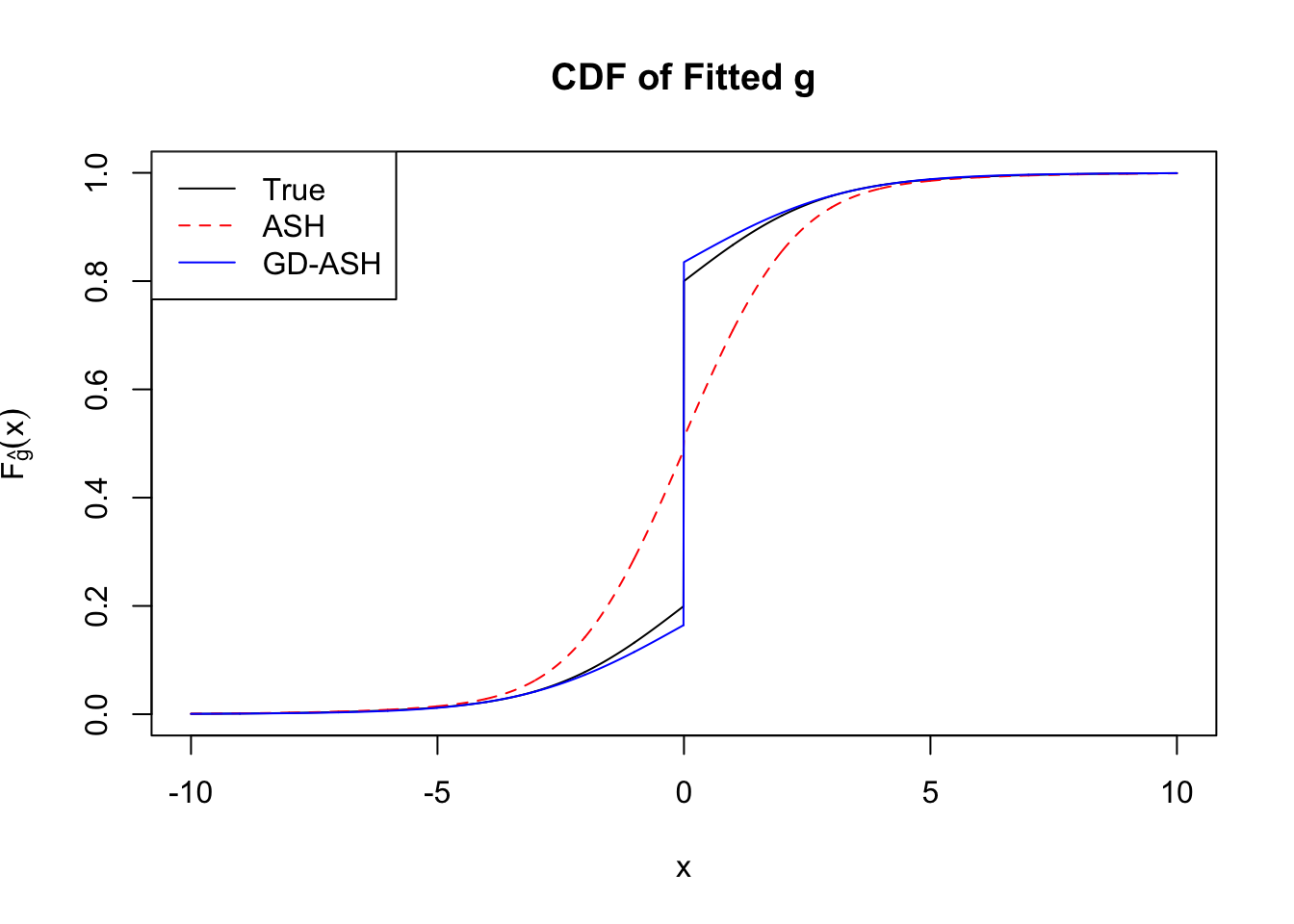
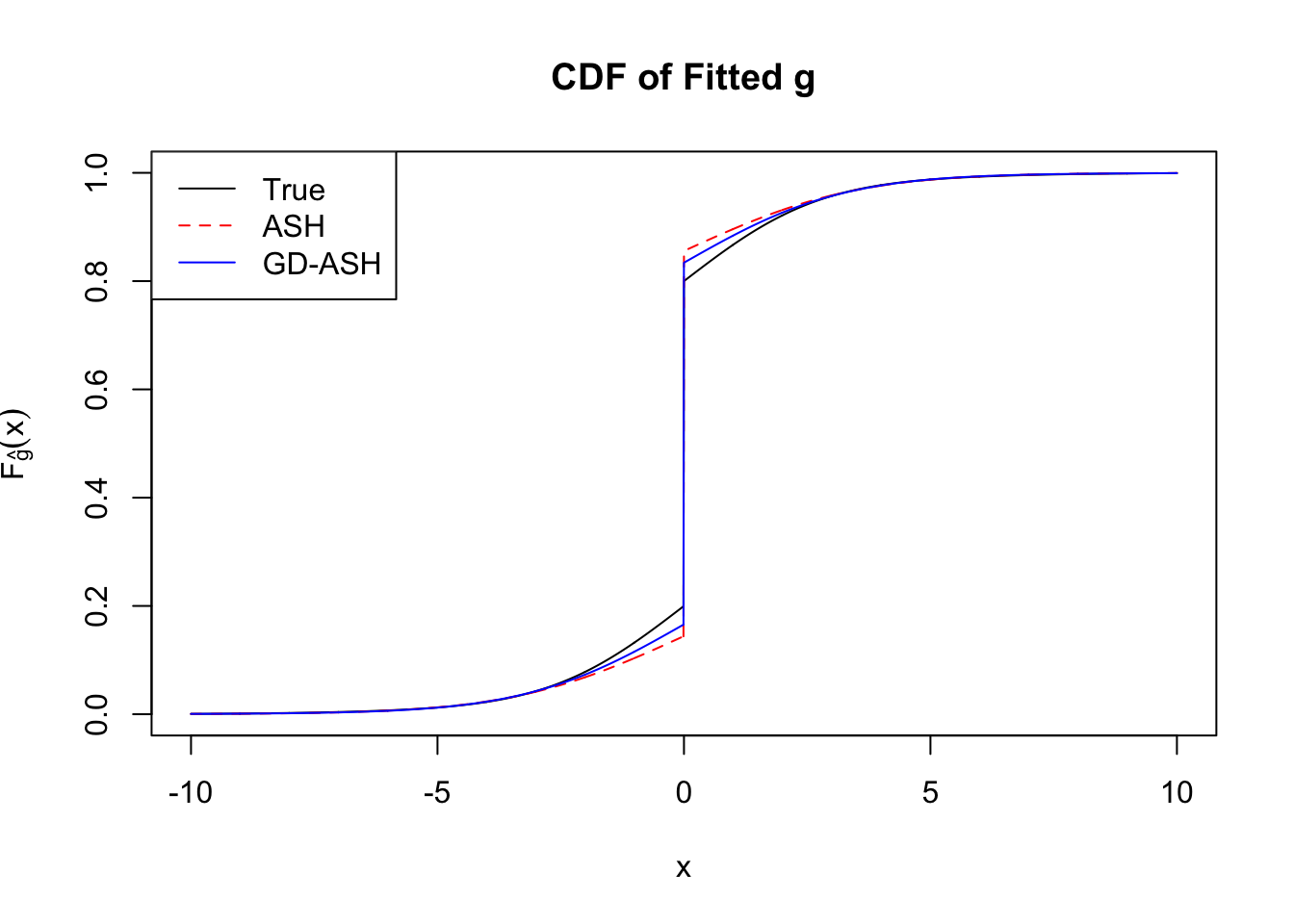
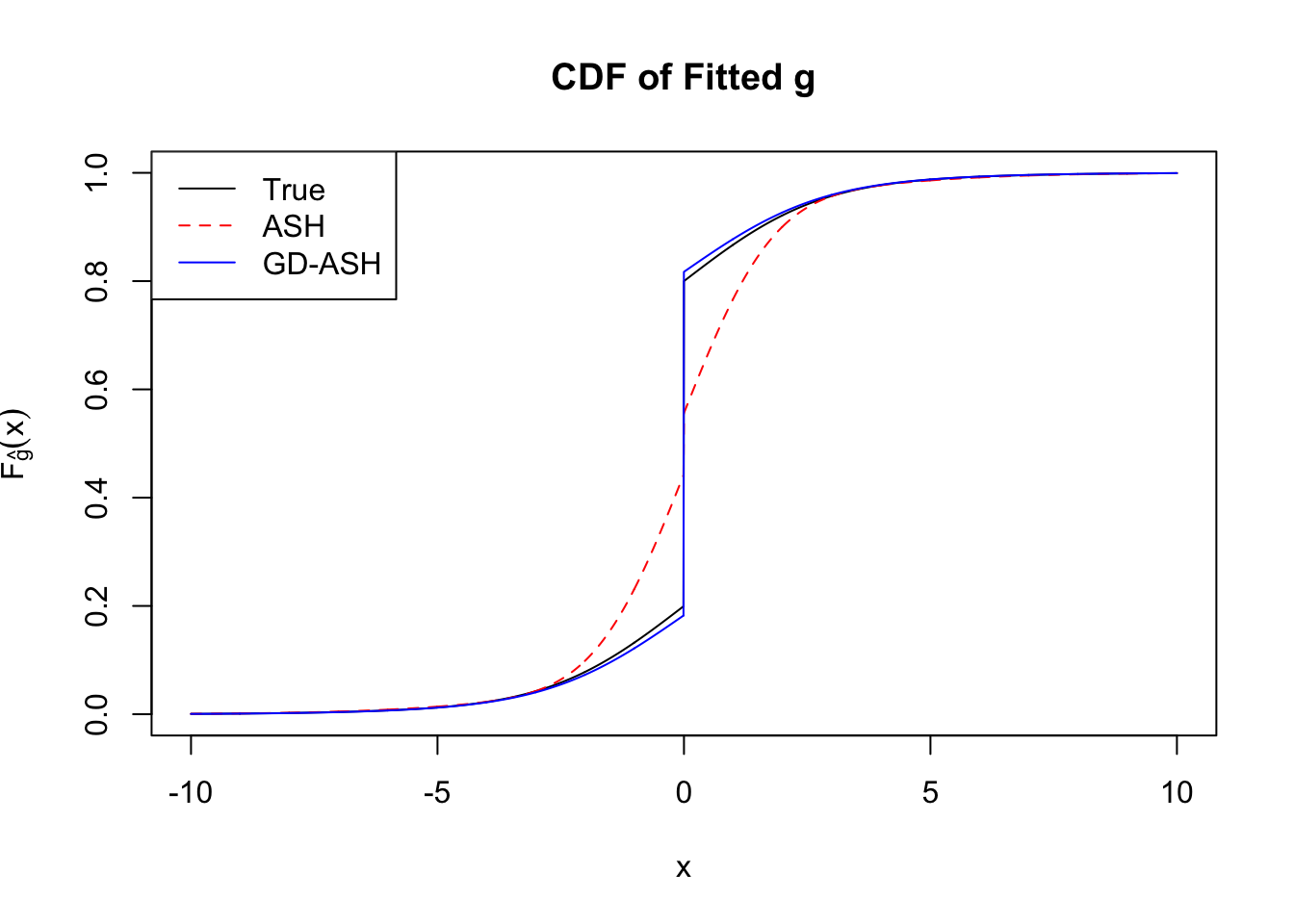
In the following, we’ll take a look at the basic form in its primal and dual formulations, optimized by w.mosek() and w.mosek.primal functions. First, they are applied to the correlated null, and their performance can be compared with the previous implementation by cvxr. Then, they are applied to the simulated non-null data sets, and the results are compared with those obtained by ASH, as well as the truth.

Basic form: primal

In its most basic form, the \(w\) estimation problem is as follows.

\[ \begin{array}{rl} \min\limits_{w} & -\sum\limits_{j = 1}^n \log\left(\sum\limits_{l=1}^Lw_l a_{jl} + a_{j0}\right) \\ \text{subject to} & \sum\limits_{l=1}^Lw_l a_{jl} + a_{j0} \geq 0, \forall j \ .\\ \end{array} \] Let the matrix \(A = \left[a_{jl}\right]\), the vector \(a = \left[a_{j0}\right]\), and we have its equivalent form,

\[ \begin{array}{rl} \min\limits_{w, g} & -\sum\limits_{j = 1}^n \log\left(g_j\right) \\ \text{subject to} & Aw + a = g \\ & g \geq 0\ . \end{array} \]

This problem can be coded by Rmosek as a “separable convex optimization” (SCOPT) problem.

Correlated null

Fitted w: -0.03653526 0.1999284 0.01047094 -0.02012681 
Time Cost in Seconds: 7.945 2.884 13.152 

Fitted w: 0.03394291 0.7345604 -0.1532514 0.1883912 -0.05504895 0.02297176 -0.006908406 0.001216017 -0.0003147927 
Time Cost in Seconds: 6.902 1.98 6.669 

Fitted w: 0.02262546 0.9213963 0.02180428 0.1760983 -0.01379674 0.003968132 -0.004904973 -0.0006085249 -0.0002990675 
Time Cost in Seconds: 5.375 1.932 6.116 

Fitted w: 0.04540484 -0.1275978 0.009150985 0.01004515 
Time Cost in Seconds: 19.294 2.066 14.959 

Fitted w: 0.005943196 0.3980709 -0.009222458 0.02630697 
Time Cost in Seconds: 6.636 1.954 6.815

Signal \(+\) correlated error

Converged: FALSE 
Number of Iteration: 101 
Time Cost in Seconds: 2181.997 255.051 1644.499 

Converged: FALSE 
Number of Iteration: 101 
Time Cost in Seconds: 2634.559 296.365 1970.452 

Converged: TRUE 
Number of Iteration: 45 
Time Cost in Seconds: 553.188 127.588 540.733 

Converged: TRUE 
Number of Iteration: 49 
Time Cost in Seconds: 781.062 126.839 622.938 

Converged: FALSE 
Number of Iteration: 101 
Time Cost in Seconds: 2161.426 247.628 1565.216

Basic form: dual

The primal \(w\) optimization problem has \(n + L\) variables and \(n\) constraints. When \(n\) is large, such as \(n = 10K\) in our simulations, the time cost is usually substantial. As the authors of REBayes pointed out, it’s better to work on the dual form, which is

\[ \begin{array}{rl} \min\limits_{v} & -\sum\limits_{j = 1}^n \log\left(v_j\right) + a^Tv \\ \text{subject to} & A^Tv = 0 \\ & v \geq 0\ . \end{array} \] The dual form has \(n\) variables and more importantly, only \(L\) constraints. As \(L \ll n\), the dual form is far more computationally efficient.

Rmosek provides optimal solutions to both primal and dual variables, so \(\hat w\) is readily available when working on \(v\) optimization. But we need to be careful on which dual variables to use, such as $sol$itr$suc, $sol$itr$slc, or others.

Correlated null

Fitted w: -0.03642797 0.1971637 0.01074601 -0.02181494 
Time Cost in Seconds: 0.485 0.049 0.388 

Fitted w: 0.03361434 0.7339189 -0.1544144 0.1875235 -0.0560049 0.02267003 -0.007151714 0.001187682 -0.0003321398 
Time Cost in Seconds: 0.524 0.009 0.372 

Fitted w: 0.02273596 0.9206369 0.02224234 0.1750273 -0.01339113 0.003607418 -0.004794795 -0.0006395078 -0.0002908422 
Time Cost in Seconds: 0.529 0.008 0.375 

Fitted w: 0.04544396 -0.1272823 0.008811108 0.009915311 
Time Cost in Seconds: 0.448 0.006 0.322 

Fitted w: 0.006084177 0.3976595 -0.009103231 0.02610567 
Time Cost in Seconds: 0.489 0.005 0.313

Signal \(+\) correlated error

Converged: TRUE 
Number of Iteration: 21 
Time Cost in Seconds: 46.978 2.71 29.017 

Converged: TRUE 
Number of Iteration: 21 
Time Cost in Seconds: 45.406 5.343 52.01 

Converged: TRUE 
Number of Iteration: 16 
Time Cost in Seconds: 34.293 3.519 26.79 

Converged: TRUE 
Number of Iteration: 31 
Time Cost in Seconds: 64.198 3.902 39.897 

Converged: TRUE 
Number of Iteration: 12 
Time Cost in Seconds: 27.247 1.446 15.392

Conclusion

Implementation by Rmosek can fully reproduce the results obtained by cvxr. Moreover, the dual form gives the same results as the primal dorm does, with only a fraction of time.

It seems hopeful that we’ll find a key to successfully tackle correlation in simultaneous inference, which has eluded Prof. Brad Efron for more than a decade.

Session information

sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] Rmosek_8.0.69     PolynomF_1.0-1    CVXR_0.94-4       REBayes_1.2      
[5] Matrix_1.2-12     SQUAREM_2017.10-1 EQL_1.0-0         ttutils_1.0-1    

loaded via a namespace (and not attached):
 [1] Rcpp_0.12.14      knitr_1.17        magrittr_1.5     
 [4] bit_1.1-12        lattice_0.20-35   R6_2.2.2         
 [7] stringr_1.2.0     tools_3.4.3       grid_3.4.3       
[10] R.oo_1.21.0       git2r_0.20.0      scs_1.1-1        
[13] htmltools_0.3.6   bit64_0.9-7       yaml_2.1.16      
[16] rprojroot_1.3-1   digest_0.6.13     gmp_0.5-13.1     
[19] ECOSolveR_0.3-2   R.utils_2.6.0     evaluate_0.10.1  
[22] rmarkdown_1.8     stringi_1.1.6     compiler_3.4.3   
[25] Rmpfr_0.6-1       backports_1.1.2   R.methodsS3_1.7.1

This R Markdown site was created with workflowr