Semicircular correlated \(z\) scores

Data generation

Let \(L_{n \times k} = \left[L_{ij}\right]_{n \times k}\) be a matrix, each entry of which is generated as follows.

1. Let \(L_{ij} \sim N(0, 1)\) independently.
2. Let \(L_{ij} = \displaystyle\frac {L_{ij}}{\sqrt{L_{i1}^2 + \cdots + L_{ik}^2}}\). That is, normalizing each row so that each row has a unit \(l_2\) norm.

Then taking \(L\) as known, let \(x \sim N\left(0, I_k\right)\) be a \(k\)-dimensional vector comprised of \(k\) independent \(N\left(0, 1\right)\) random variables. Then \[ z = Lx \sim N\left(0, LL^T\right) \] should be \(n\) marginally \(N\left(0, 1\right)\) but correlated \(z\) scores. Indeed, \[ \begin{array}{c} \text{var}\left(z_i\right) = l_i^Tl_i = 1 \ ; \\ \text{cov}\left(z_i, z_j\right) = l_i^Tl_j \neq 0 \text{, in general} \ ; \end{array} \] where \(l_i^T\) and \(l_j^T\) are \(i^\text{th}\) and \(j^\text{th}\) rows of \(L\) respectively.

Then we plot the histogram of \(n\) \(z\) scores. One interesting thing is we can prove what these histograms would look like when \(n\) is sufficiently large.

\(k = 4\)

For example, when \(k = 4\), \(n\) is sufficiently large, say, \(10^6\), the histogram of \(z\) looks like a semicircle almost perfectly, as illustrated in the following simulation. The semicircle is centered at the origin, and has a radius of \(\left\|x\right\|_2\).

set.seed(1)
n = 1e6
k = 4
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)
R = sqrt(sum(x^2))
x.plot = seq(-max(abs(z)) - 1, max(abs(z)) + 1, length = 1000)
y.plot = 2 * sqrt(pmax(R^2 - x.plot^2, 0)) / (pi * R^2)
lines(x.plot, y.plot, col = "red")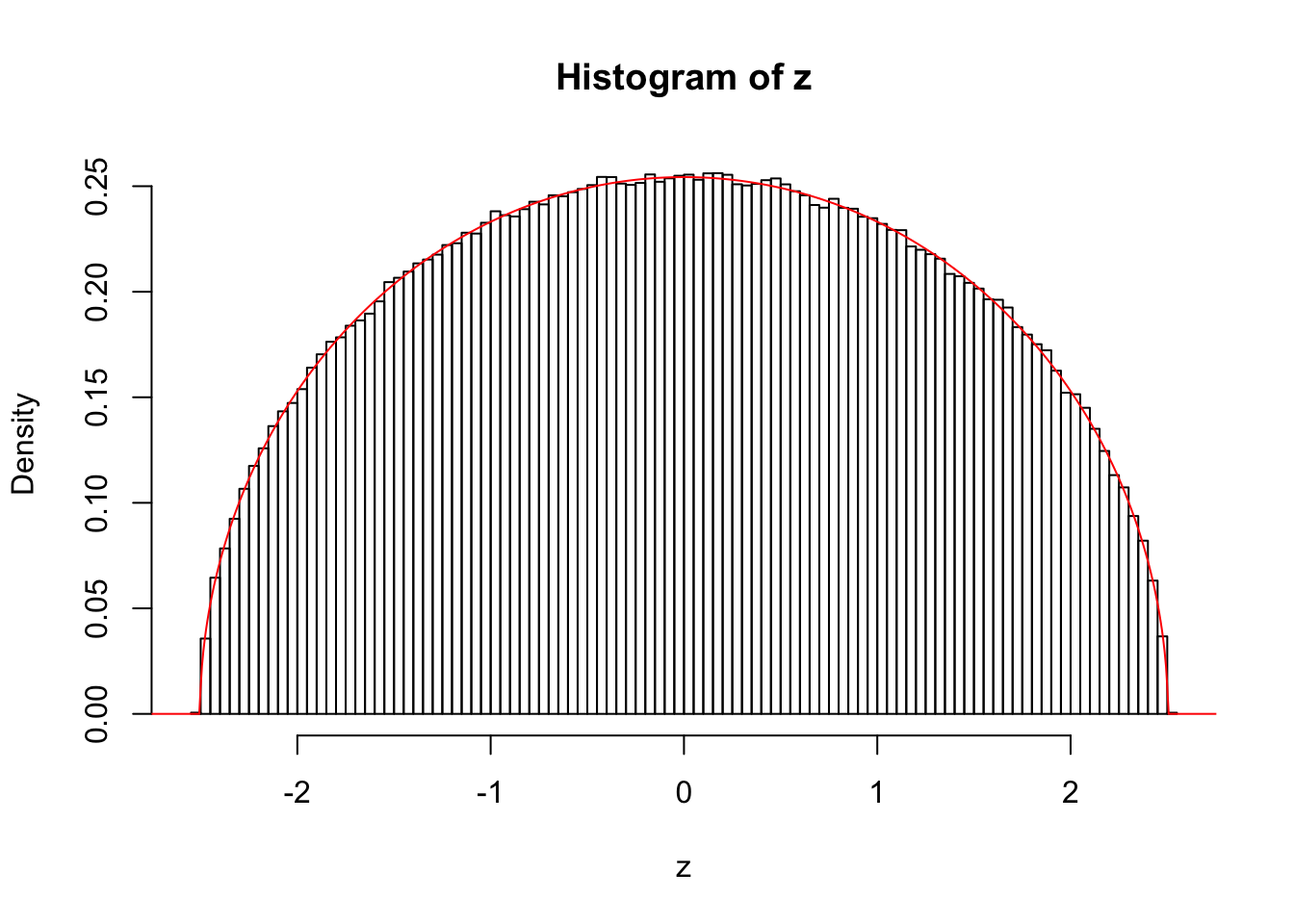

Actually, when \(k \neq 4\), for example, \(k = 3\) or \(k = 5\), the histograms of these correlated \(z\) scores, simulated the same way, look different, and their shapes when \(n \to \infty\) can be mathematically determined.

\(k = 3\)

set.seed(1)
n = 1e6
k = 3
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)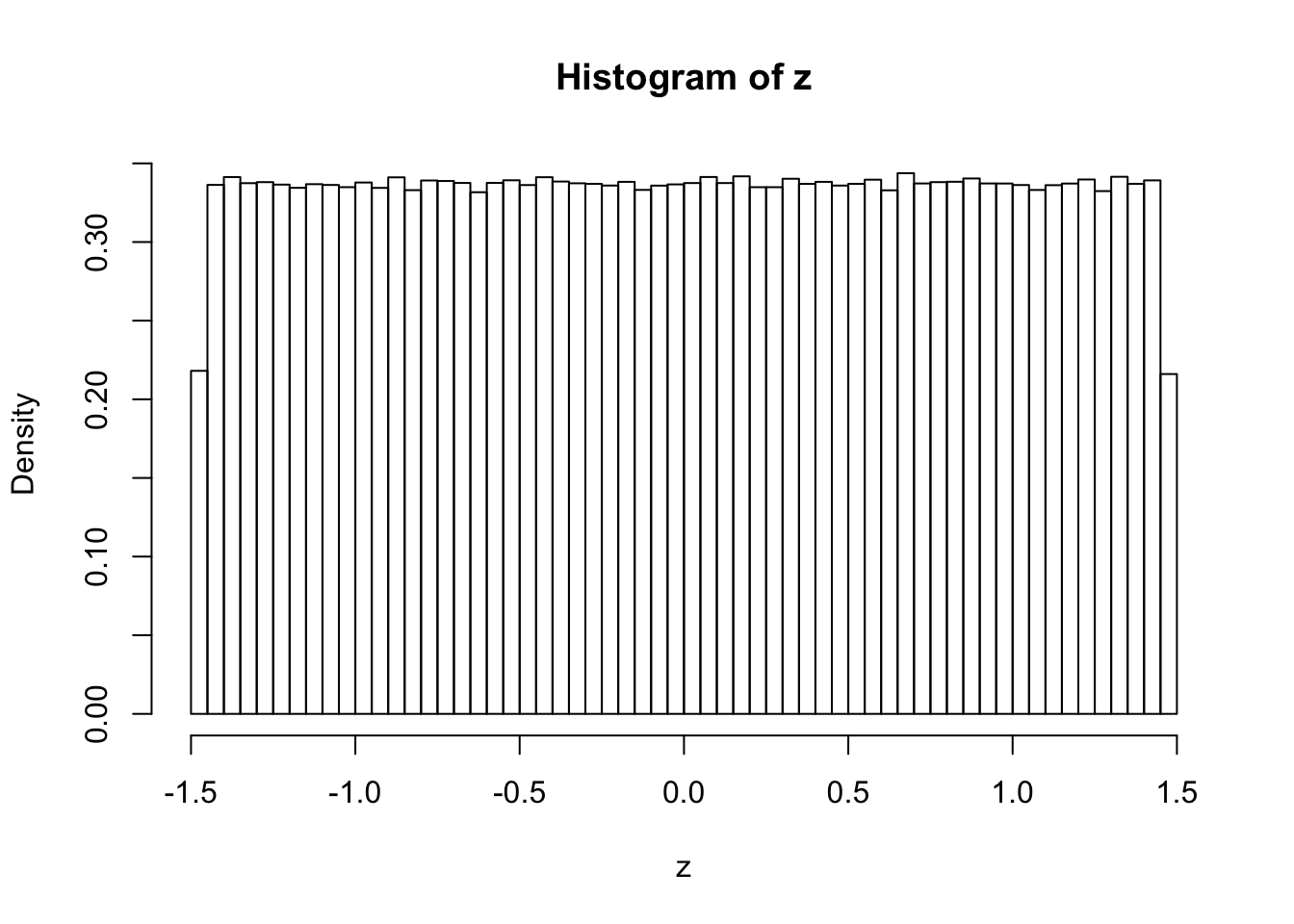

\(k = 5\)

set.seed(1)
n = 1e6
k = 5
L = matrix(rnorm(n * k), nrow = n)
s = sqrt(rowSums(L^2))
L = L / s
x = rnorm(k)
z = L %*% x
hist(z, breaks = 100, prob = TRUE)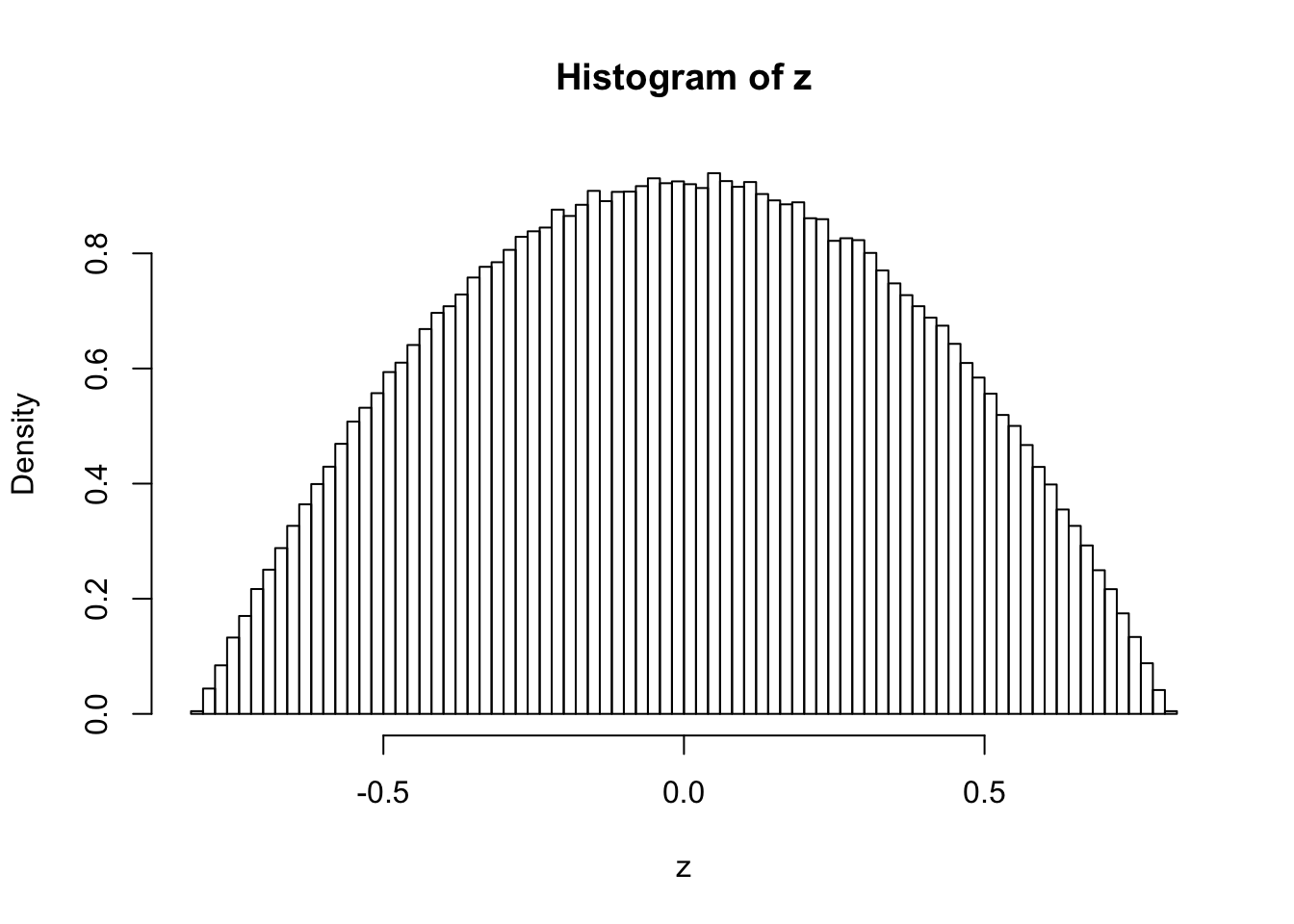

Session information

sessionInfo()

R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2

Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

loaded via a namespace (and not attached):
 [1] compiler_3.4.3  backports_1.1.2 magrittr_1.5    rprojroot_1.3-1
 [5] tools_3.4.3     htmltools_0.3.6 yaml_2.1.16     Rcpp_0.12.14   
 [9] stringi_1.1.6   rmarkdown_1.8   knitr_1.17      git2r_0.20.0   
[13] stringr_1.2.0   digest_0.6.13   evaluate_0.10.1