Rmosek: Primal vs Dual
Lei Sun
2017-06-21
Last updated: 2017-12-21
Code version: 6e42447
Introduction
It has been noted that in the specific maximum likelihood estimation problem, optimization runs faster in the dual form than in the primal one. We are testing that with a simple numeric example.
Problem
Let \(A_{n \times m}\) be a matrix with \(n \gg m\) and \(a\) an \(n\)-vector. The prototypical convex optimization problem in my applications is
\[
\begin{array}{rl}
\min\limits_{f \in \mathbb{R}^m, \ \ g \in \mathbb{R}^n} & -\sum\limits_{i = 1}^n\log\left(g_i\right) \\
\text{s.t.} & Af + a = g\\
& g \geq 0 \ .
\end{array}
\] Note here the only reason we are adding the latent variable \(g\) is that in this way we can code the problem using Rmosek::mosek as a “separable convex optimization” (SCOPT) problem.
Its dual form is
\[ \begin{array}{rl} \min\limits_{\nu \in \mathbb{R}^n} & a^T\nu-\sum\limits_{i = 1}^n\log\left(\nu_i\right) \\ \text{s.t.} & A^T\nu = 0\\ & \nu\geq0 \ . \end{array} \]
The idea is that when \(n \gg m\), the dual optimization should be much faster than the primal one using Rmosek::mosek.
Comparison
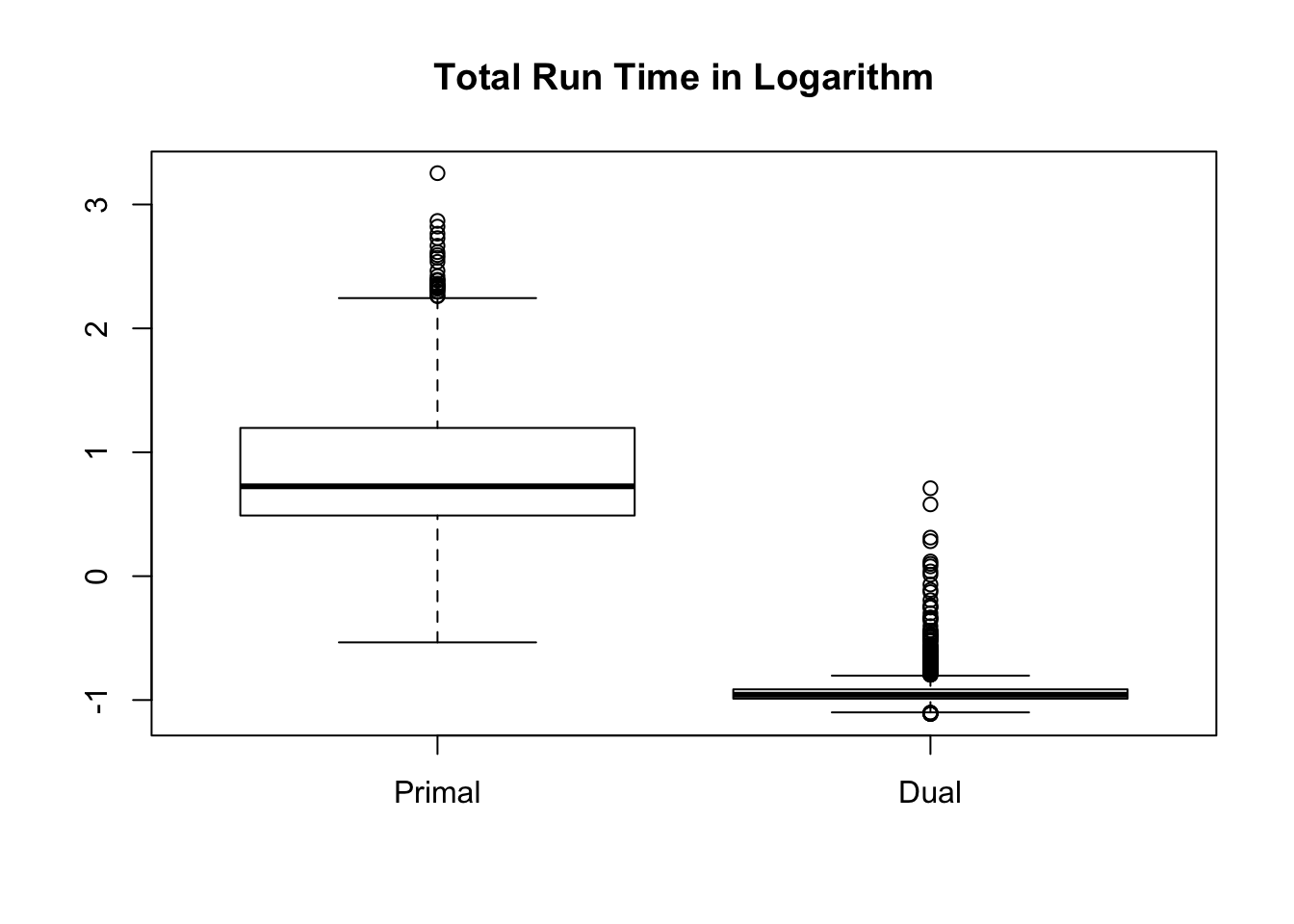
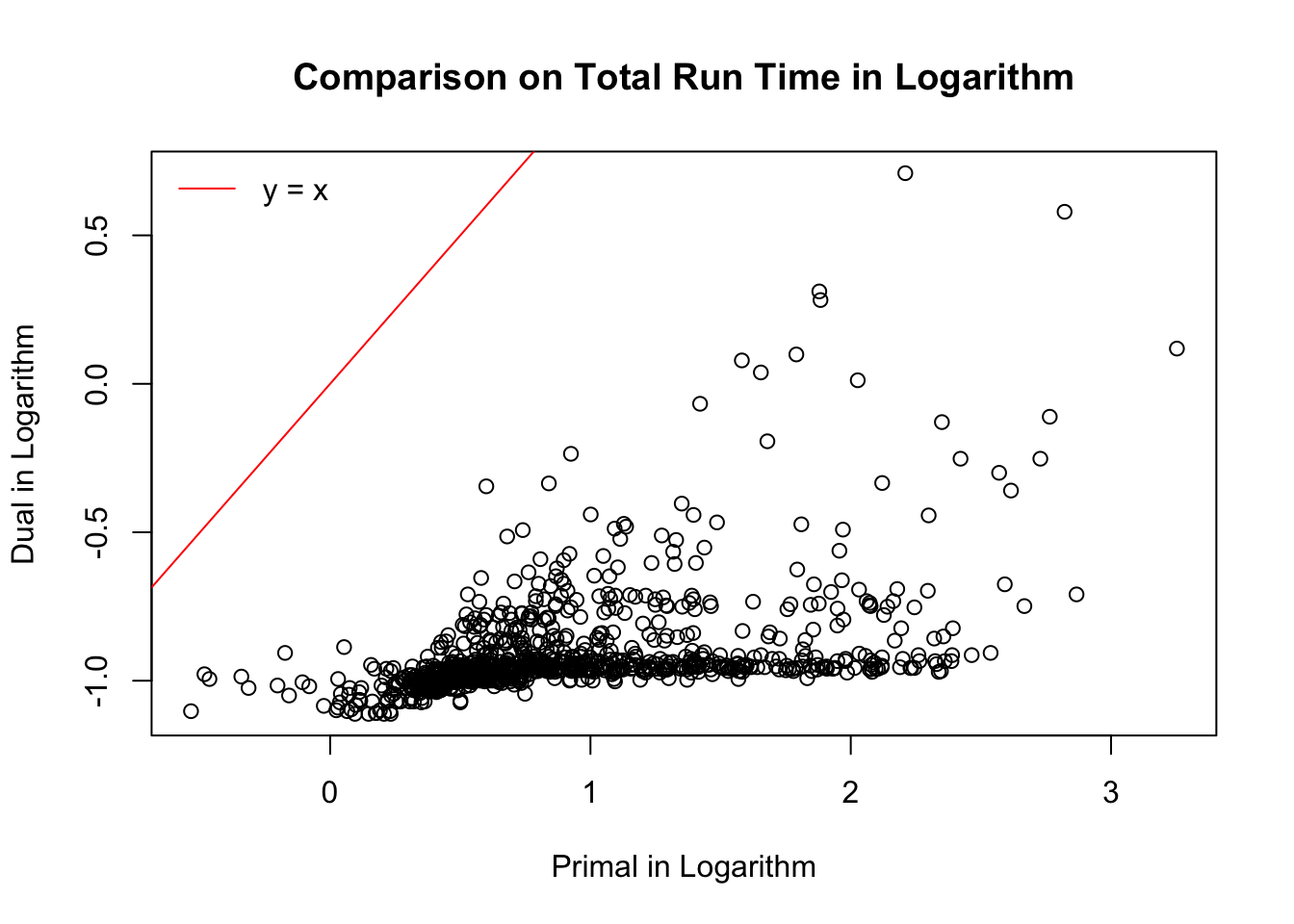
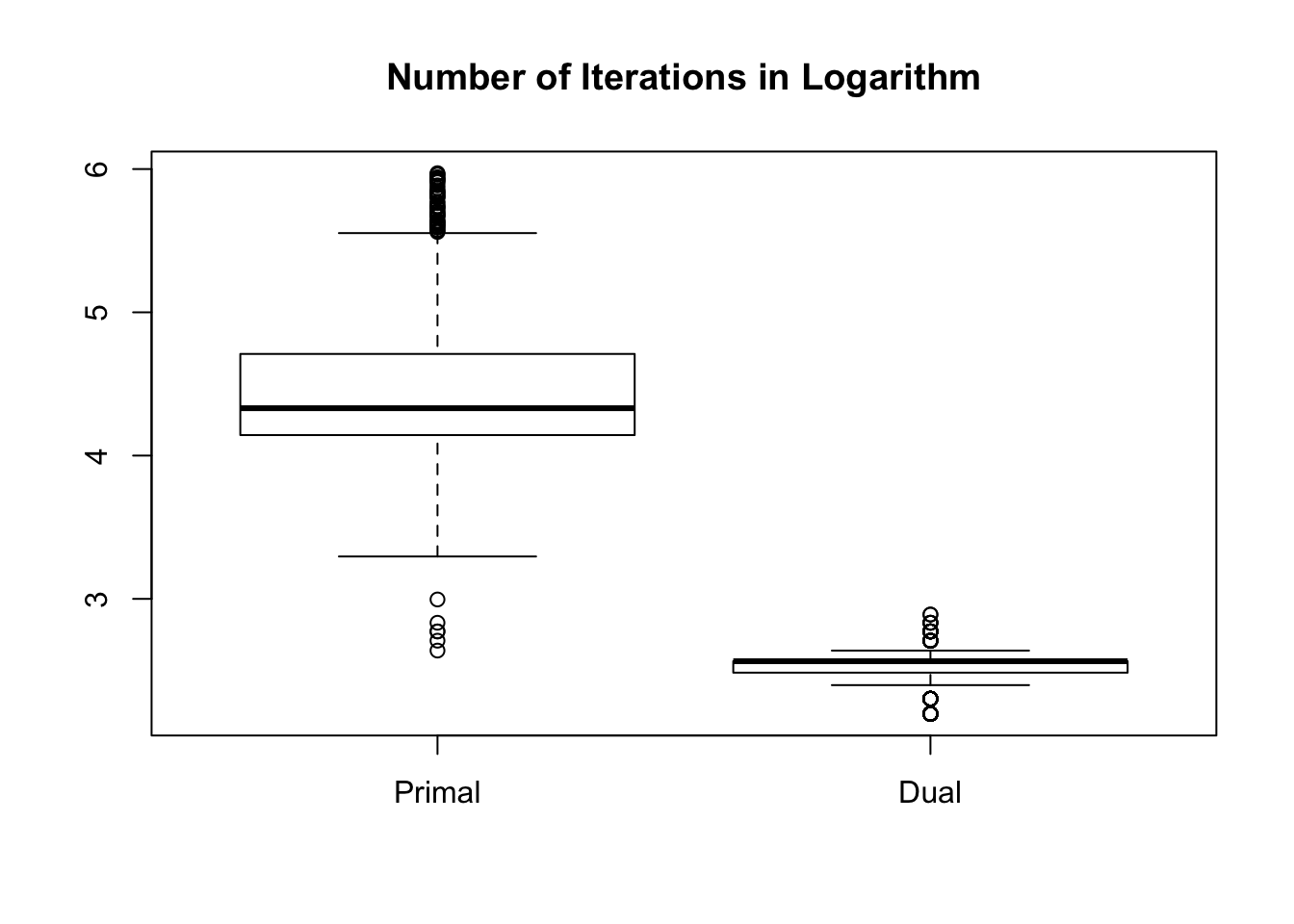
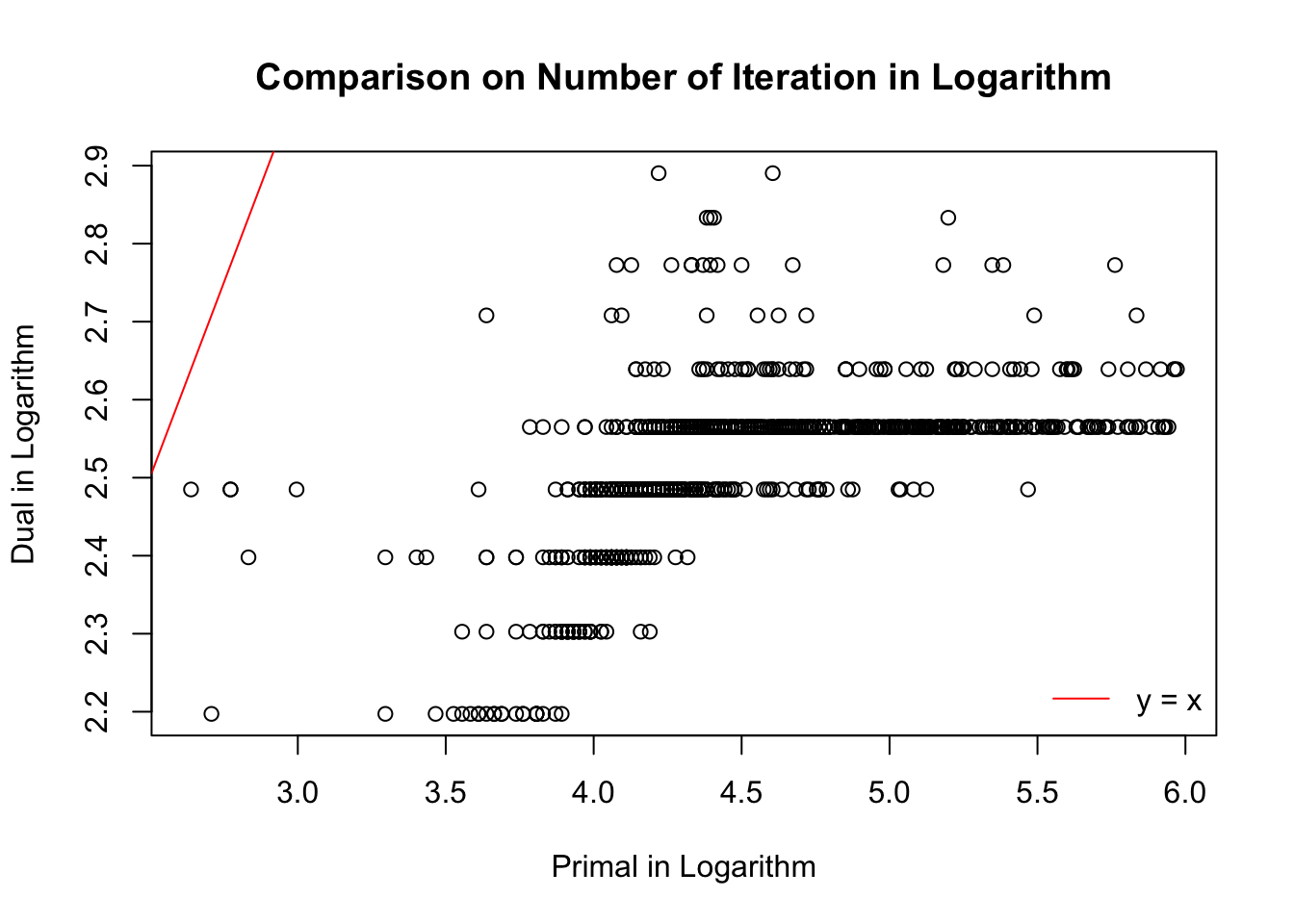
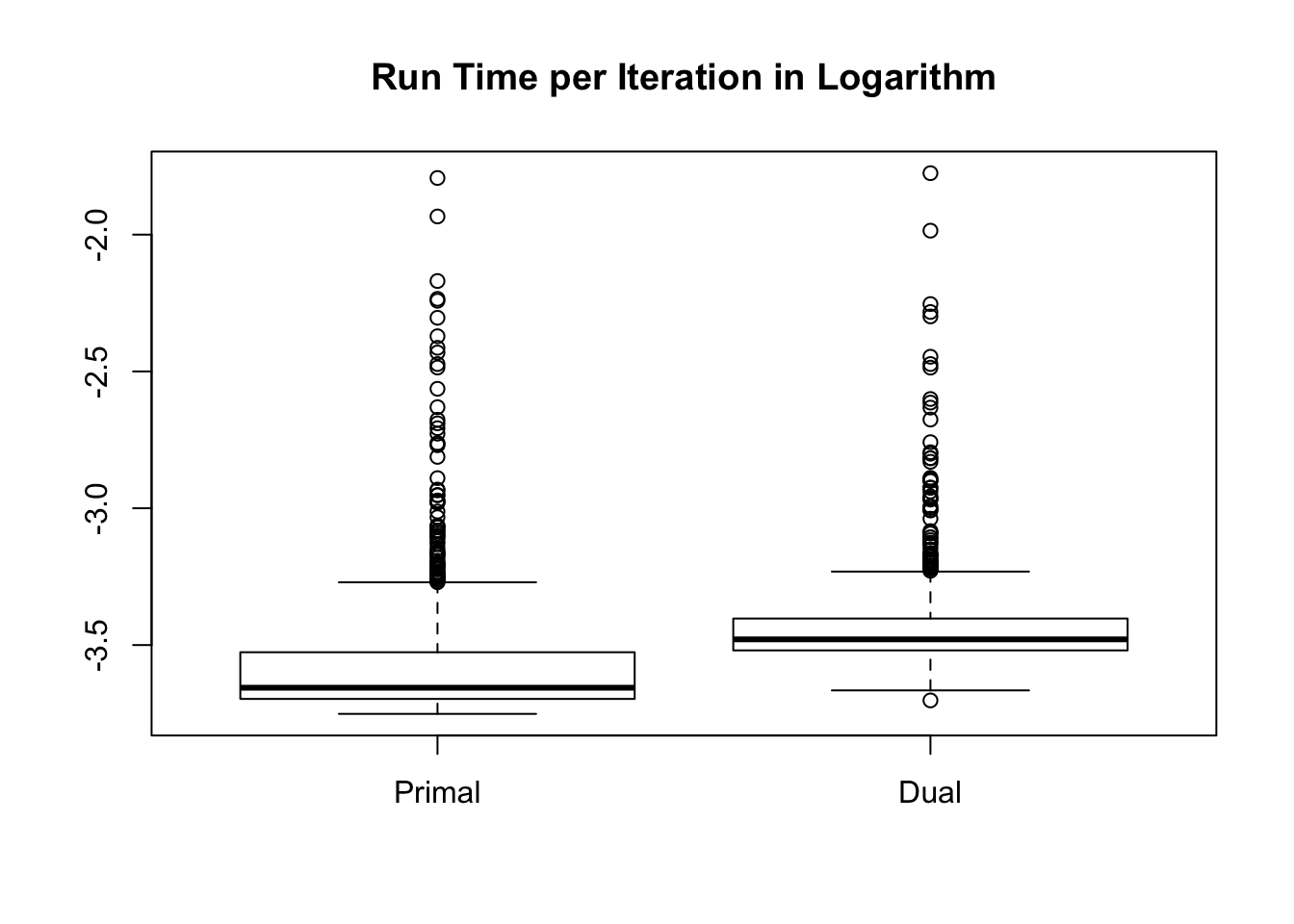
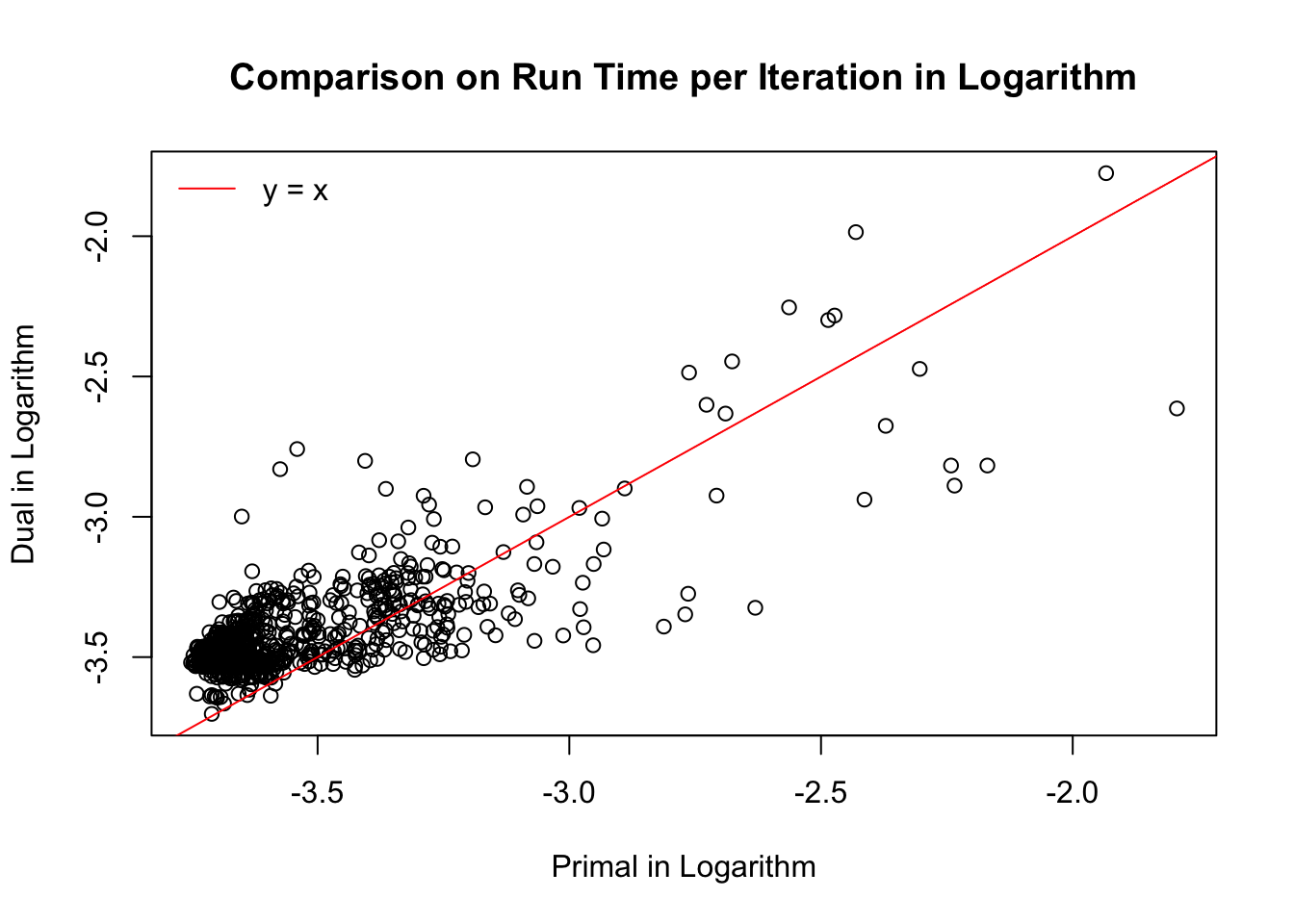
Let \(n = 10^4\), \(m = 10\), so that indeed \(n \gg m\). We run \(1000\) simulation trials. In each trial we feed the primal and the dual with the same \(A\) and \(a\). \(A\) and \(a\) are generated so that both the primal and dual problems are feasible at least in theory. Now we are comparing accuracy, time cost, and numbers of iterations of the two forms.
In the following comparisons, we only compare the results when both primal and dual reach the optimal. Worthnoting is that out of \(1000\) runs, the dual reaches optimal in all of them, whereas the primal doesn’t in 61 of them, or \(6.1\%\).
Total time cost
Number of iterations
Time per iteration
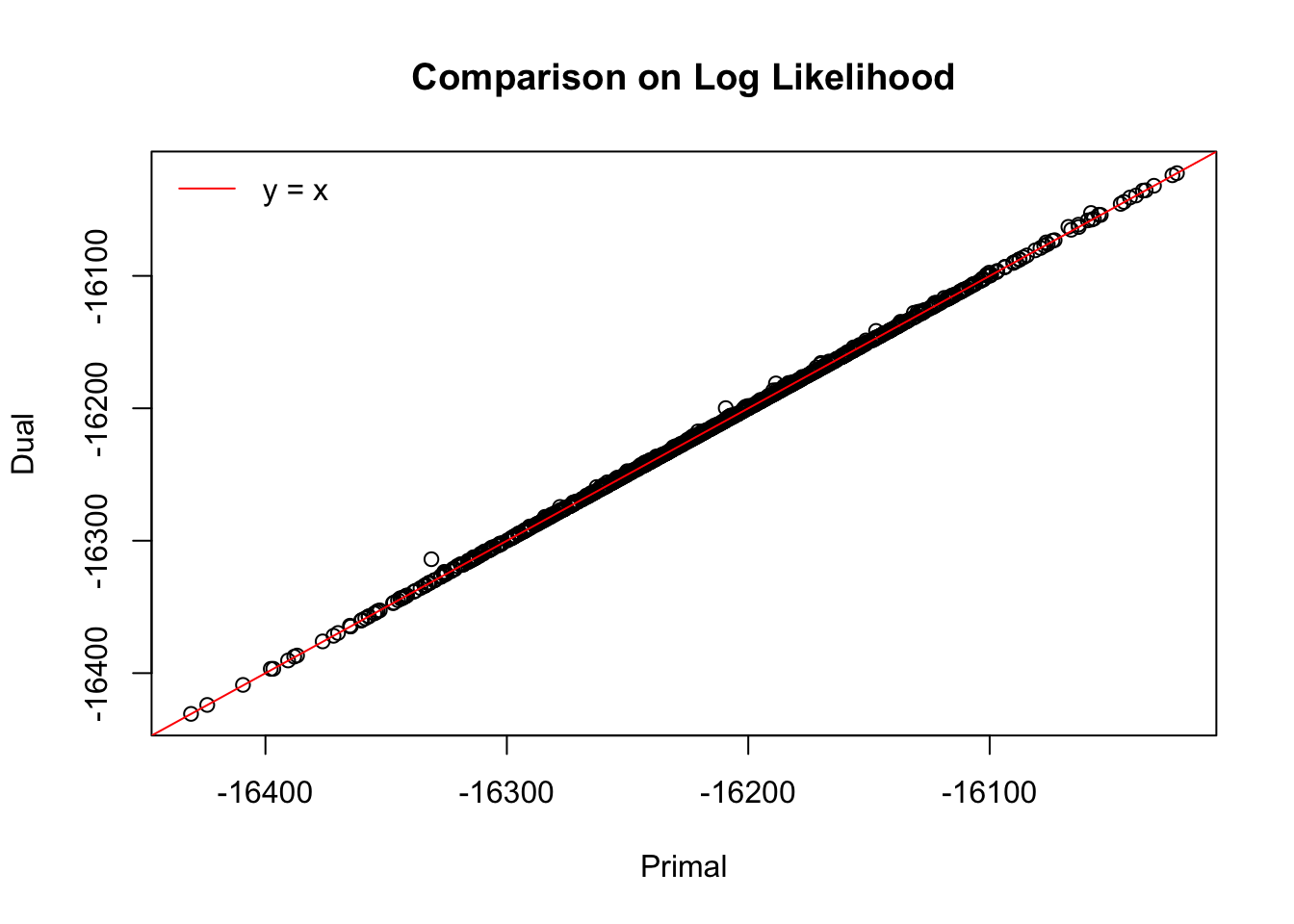
Log likelihood
It appears the dual form also gives better results in the sense that the log-likelihood given by dual is larger than the log-likelihood given by primal, when both reach the optimal. For both forms, the log-likelihood is given by \(\sum\log\left(Af + a\right) = \sum\log\left(g\right)\).
Session information
sessionInfo()R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS High Sierra 10.13.2
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] compiler_3.4.3 backports_1.1.2 magrittr_1.5 rprojroot_1.3-1
[5] tools_3.4.3 htmltools_0.3.6 yaml_2.1.16 Rcpp_0.12.14
[9] stringi_1.1.6 rmarkdown_1.8 knitr_1.17 git2r_0.20.0
[13] stringr_1.2.0 digest_0.6.13 evaluate_0.10.1This R Markdown site was created with workflowr